加密算法之RSA(一)

张彤 2021年10月31日 1,152次浏览

对于服务器部署在云或者公网上的情况，登录方式一般都不会采用简单的密码登录。
可以使用以下命令查看不同ip猜密码的情况

cat /var/log/secure

当然，你可以在云端限制ip，然而更好的办法是使用密钥登录。

centos7 密钥登录

本文不是介绍如何添加及使用密钥的，而是密码学里一个非常有趣的算法，RSA。

  • RSA 中文名称公钥加密算法，可以这样说，它是现代计算机通讯安全的基石。

在1976年之前，即便是复杂的英格玛机（一种二战德国的加密机器）也要服从以下两条原则

1, Alice使用一种特定的加密规则对信息加密
2，Bob如果想要解密，则需要知道Alice的机密规则

这种加密方法，统称为对称加密。

那么，麻烦也就是来了，保存和传递密钥就成了大难题。
天天换密钥也是有风险的，当Alice每天把密钥发给Bob时，如果这把钥匙是每天更换还好，如果连续几周不更换，那么密文被破译的几率将会几何倍数增加。

难道从凯撒密码到英格玛机，人类的加密办法穷尽了吗？
当然不可能了！
1976年，两位美国计算机学家Whitfield Diffie 和 Martin Hellman，提出了大名鼎鼎的迪菲赫尔曼交换密钥算法。
这个时候，人们意识到加密和解密是可以使用不同规则进行的。

这种办法被成为 非对称加密

1977年，三位数学家Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。
RSA算法也是三位大神名字首字母的组合。
rsa.jpg

那么在正式介绍RSA实现方法前，需要了解一些数学知识，别紧张，只要有点数论基础就可以啦~~~

互质关系

  • 如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系，也有叫互素关系的。

需要注意的是，互质关系的两个数，不仅仅是质数，比如 3和 10 就是互质关系，但很明显，10不是质数

关于互质，有以下特性

  1. 两个不同的质数一定是互质数。
  2. 一个质数，另一个不为它的倍数，这两个数为互质数。
  3. 1不是质数也不是合数，它和任何一个自然数（1本身除外）在一起都是互质数。
  4. 相邻的两个自然数是互质数.
  5. 相邻的两个奇数是互质数。
  6. 较大数是质数的两个数是互质数
  7. 两个数都是合数（二数差又较大），较小数所有的质因数，都不是较大数的约数，这两个数是互质数。
  8. 两个数都是合数（二数差较小），这两个数的差的所有质因数都不是较小数的约数，这两个数是互质数。
  9. 两个数都是合数，较大数除以较小数的余数（不为“0”且大于“ 1”）的所有质因数，都不是较小数的约数，这两个数是互质数。

判断一个数是否为质数，python实现如下:

def is_prime(a):
    return all(a % i for i in xrange(2, a))

按照互质定义，判断两个数是否互质的函数 python实现如下:

#c 接口实现，速度更快
from math import gcd as bltin_gcd
def is_coprime(a,b):
    return bltin_gcd(a,b) == 1

#不使用内置math库实现
def gcd(a, b):
    while b != 0:
        a, b = b, a % b
    return a

def coprime(a, b):
    return gcd(a, b) == 1

欧拉函数

对正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的数目。此函数以其首名研究者欧拉命名，它又称为φ函数（由高斯所命名）或是欧拉总计函数（totient function，由西尔维斯特所命名）。

在1到8之中，与8形成互质关系的是1、3、5、7，所以 φ(n) = 4。

欧拉函数的值讨论

  1. 第一种情况
    φ(1)=1（小于等于1的正整数中唯一和1互质的数就是1本身）
  2. 第二种情况
    如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系。比如5与1、2、3、4都构成互质关系。
  3. 如果n是质数的某一个次方，即 n = pk (p为质数，k为大于等于1的整数)
    $$\phi(p    k) = pk - p$$
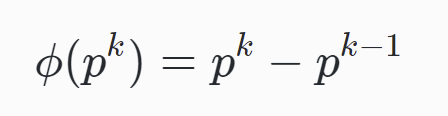
    欧拉函数1.png
  4. 如果n可以分解成两个互质的整数之积
    $$\because n = p_1 \times p_2$$
    $$\therefore \phi(n) = \phi(p_1p_2) = \phi(p_1)\phi(p_2)$$
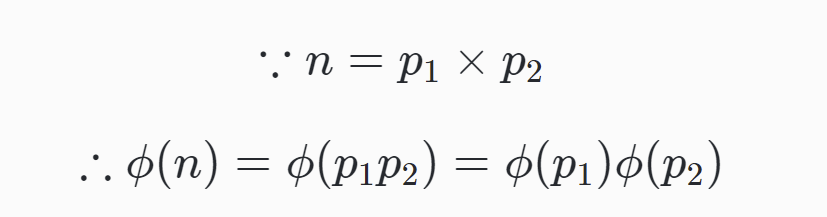
    欧拉函数2.png
    即积的欧拉函数等于各个因子的欧拉函数之积。比如，φ(56)=φ(8×7)=φ(8)×φ(7)=4×6=24。
  5. 由4 可以推广出 欧拉函数是积性函数，这也是RSA的基础。
    因为任意一个大于1的正整数，都可以写成一系列质数的积。
  • $$ n = p_1p_2p_3\cdots p_r $$
  • $$ \phi(n) = \phi(p_1)\phi(p_2)\phi(p_3) \cdots \phi(p_r)$$
  • $$\phi(n) = p_1p_2p_3\cdots p_r(1 -\frac1)(1 -\frac1)(1 -\frac1) \cdots(1 -\frac1)$$
  • $$ \phi(n) = n (1 -\frac1)(1 -\frac1)(1 -\frac1) \cdots(1 -\frac1)$$

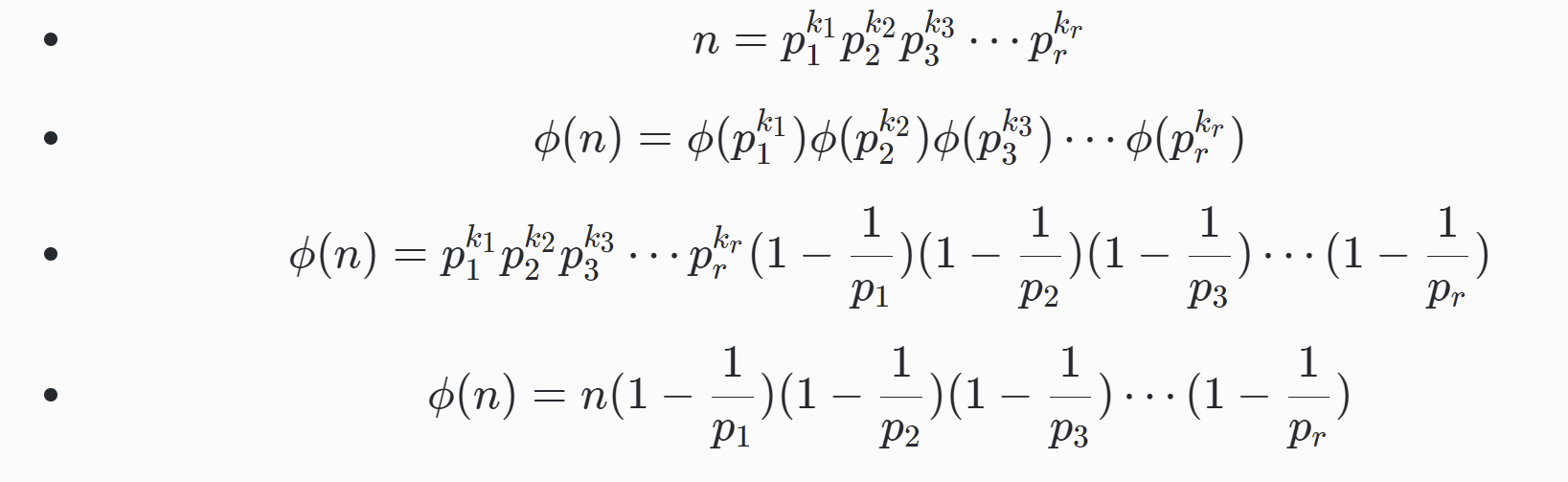
欧拉函数3.png

具体的推导过程大家可以结合2，3步进行理解。
关于欧拉函数是积性函数的证明，可以参考以下链接

欧拉函数的性质

欧拉函数的python实现

from math import gcd

def phi(n):
    amount = 0        
    for k in range(1, n + 1):
        if gcd(n, k) == 1:
            amount += 1
    return amount

欧拉定理

既然知道了欧拉函数，那么它有什么用呢？
它的用处在于欧拉定理。
欧拉定理定义如下

  • 如果两个正整数a和n互质(gcd(a,n)=1)，则n的欧拉函数 φ(n) 可以让下面的等式成立
    $$a^{\varphi(n)}\equiv 1 (\mod n) $$
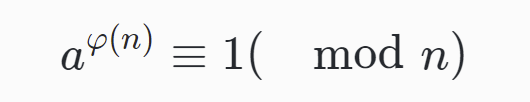
    欧拉定理1.png
    a的φ(n)次方减去1，可以被n整除
    欧拉定理的证明涉及群论，比较复杂，有兴趣的同学可以深入了解一下，参考链接：

Euler’s Theorem: proof by modular arithmetic

欧拉定理的重要作用在于

很大程度地简化幂的模运算

欧拉定理的一个特例，就是费马小定理
假设正整数a与质数p互质，因为质数p的φ( p)等于p-1，则欧拉定理可以写成
$$a^ = 1(\mod p)$$
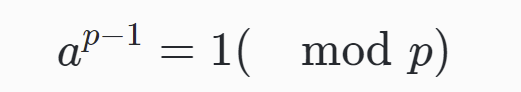
欧拉定理2.png
欧拉定理是RSA算法的核心，理解这个定理，对于理解RSA在解密端快速解密有很大帮助。

模反运算 / 模逆元

如果两个正整数a和n互质，
那么一定可以找到整数b，使得 ab-1 被n整除，
或者说ab被n除的余数是1
$$ab\equiv1(\mod n)$$
模逆.png
比如:3和11互质，那么3的模反元素就是4，因为 (3 × 4)-1 可以被11整除。

显然，模反元素不止一个， 4加减11的整数倍都是3的模反元素 ，
即如果b是a的模反元素，则 b+kn 都是a的模反元素。

python 实现模逆元

def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)

def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
        raise Exception('modular inverse does not exist')
    else:
        return x % m

ok，数学知识补充了一大堆,下一篇文章，
开始介绍RSA算法的具体实现方法！~

上一篇： 加密算法之RSA(二)