基尔霍夫电流定律

Kirchhoff’s Current Law

基尔霍夫电流定律 (KCL) 是基尔霍夫的第一定律，涉及进入与离开节点junction的电荷守恒。

要确定电路中电流的大小，我们需要使用一些定律或规则，将这些电流写成方程形式。用于网络方程的就是基尔霍夫定律，由于我们关注的是电路电流，所以这里使用基尔霍夫电流定律 (KCL)。

古斯塔夫·基尔霍夫的电流定律是电路分析的基本定律之一。该定律指出，对于并联路径，流入电路节点的总电流恰好等于流出同一节点的总电流，因为电荷无处可失，不会丢失。

换言之，所有流入与流出节点电流的代数和必须等于零：

基尔霍夫的这一思想通常称为“电荷守恒”，因为电流在节点处得到保留，没有损失。下面让我们看一个将基尔霍夫电流定律应用于单一节点的简单例子。

单一节点示例

A Single Junction

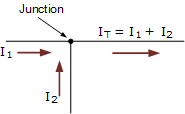
在这个简单的单一节点例子中，流出节点的电流 I_T 等于两个流入节点的电流 I_1 和 I_2 的代数和：

也可以写成代数和形式：

如果 I_1 = 3\,\mathrm{A} 且 I_2 = 2\,\mathrm{A}，那么流出节点的总电流就是

该基本定律可用于任意多个节点，因为流入和流出节点的电流总和始终相等。

此外，如果我们将电流方向反向，上述方程仍然成立：

因此，我们可以将流入节点的电流视为正值 (+)，而将流出节点的电流视为负值 (–)。不管电流方向如何，流入或流出的电流代数和始终等于零，这就是基尔霍夫节点定律，通常称为基尔霍夫电流定律 (KCL)。

并联电阻

Resistors in Parallel

下面我们来看如何将基尔霍夫电流定律应用到并联电阻电路中，无论各分支电阻是否相等。请考虑下列电路图：

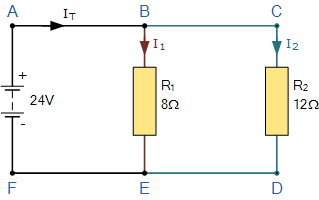
在这个简单的并联电阻示例中，有两个不同的电流节点。第一个节点出现在节点 B，第二个节点出现在节点 E。因此，我们可以对这两个不同节点处流入和流出电流，应用基尔霍夫的节点定律。

首先，所有电流 I_T 从 24 伏电源流出，到达 A 点，然后由此进入节点 B。节点 B 是一个分岔点，因为电流现在可以分成两条不同的路径：一部分电流向下通过电阻 R_1，其余电流通过节点 C 经由电阻 R_2 继续流动。注意，流入和流出节点的电流通常称为“支路电流”。

我们可以使用欧姆定律来确定每个电阻上的各支路电流，即：

因此：

对于从 B 到 E 通过电阻 R_1 的电流支路

对于通过电阻 R_2 从 C 到 D 的支路电流

由上可知，基尔霍夫电流定律指出，流入某一节点的电流总和必须等于流出该节点的电流总和。在上述简单示例中，流入节点 B 的电流为 I_T，流出该节点的电流为 I_1 和 I_2 两部分。

由于计算得出从节点 B 流出的电流为

因此流入节点 B 的电流总和为

在本例中，节点 B 和节点 E 是两个不同的分岔点，当两条支路电流在节点 E 重新汇合时，我们可以确认 I_T 的值。要使基尔霍夫节点定律成立，流入点 F 的电流总和必须等于从节点 E 流出的电流总和。

由于流入节点 E 的电流分别为 3 A 和 2 A，流入点 F 的电流总和为

即

与从点 A 流出的电流相同，因此基尔霍夫电流定律成立。

将 KCL 应用于更复杂电路时，我们仍然使用“某一节点处所有流入电流的代数和为零”的思想，关键在于区分流入节点与流出节点的电流。请参见下图电路。

基尔霍夫电流定律示例1

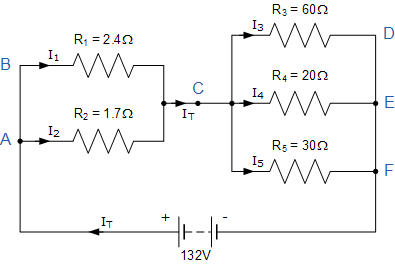
在这个示例中，在节点 A、C、E 和 F 处共有四个不同的电流分流或合流节点。电源电流 I_T 在节点 A 处分为两路，分别流经电阻 R₁ 和 R₂，随后在节点 C 重新汇合，再次通过电阻 R₃、R₄ 和 R₅ 分流，最后在节点 F 再次汇合。

但在计算每条电阻支路上的电流之前，我们必须先计算电路的总电流 I_T。欧姆定律指出：

由于已知电压 V = 132,伏，因此需要按如下方式计算电路电阻。

电路电阻 R_{AC}

Circuit Resistance R_{AC}

电路电阻 R_{CF}

因此，节点 C 与 F 之间的等效电路电阻计算为 10\ \Omega。然后，总电路电流 (I_T) 表示为：

给出一个等效电路：

基尔霍夫电流定律等效电路

Kirchhoff’s Current Law Equivalent Circuit

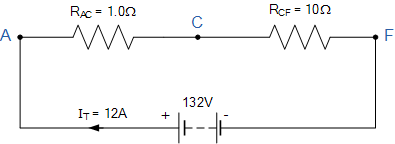
因此，V = 132\,\mathrm{V}、R_{AC} = 1\,\Omega、R_{CF} = 10\,\Omega，且 I_T = 12\,\mathrm{A}。

在已确定等效并联电阻和电源电流之后，我们现在可以计算各支路电流，并按以下方式使用基尔霍夫节点定律进行验证。

因此， I_1 = 5\ \mathrm{A}、I_2 = 7\ \mathrm{A}、I_3 = 2\ \mathrm{A}、I_4 = 6\ \mathrm{A}、I_5 = 4\ \mathrm{A}。

我们可以以节点 C 为参考点，计算流入和流出该节点的电流，以验证基尔霍夫电流定律在该电路中成立，如下：

我们还可以双重检验基尔霍夫电流定律是否成立：将流入节点的电流记为正，流出节点的电流记为负，则代数和为

即

因此，通过分析我们可以确认基尔霍夫电流定律（KCL）——“在电路网络的任一节点处，所有电流的代数和恒为零”——在本例中完全正确。

基尔霍夫电流定律示例2

仅使用基尔霍夫电流定律求解下列电路中的电流。

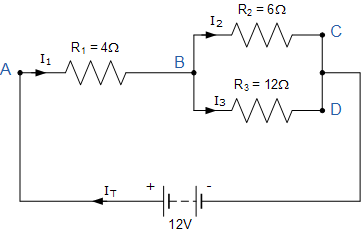
I_T 是由 12\,\mathrm{V} 电源电压驱动的整个电路中的总电流。在 A 点，I_1 = I_T，因此在电阻 R_1 上会出现 I_1R_1 的电压降。

该电路有 2 条支路、3 个节点（B、C 和 D）和 2 个独立回路，因此两个回路中的 IR 电压降为：

回路 ABC：

回路 ABD：

由于基尔霍夫电流定律指出在节点 B 处

因此我们可以将上述两个回路方程中的 I_1 用 (I_2 + I_3) 代替，然后进行简化。

基尔霍夫回路方程

现在我们得到了两个与电路中电流流动相关的联立方程：

方程 1：

方程 2：

通过将第一个方程（回路 ABC）乘以 4 并将回路 ABD 方程从回路 ABC 方程中相减，可以化简这两个方程以求出 I_2 和 I_3 的值：

方程 1（×4）：

方程 2（×1）：

方程 1 – 方程 2：

由此得：

接着，用同样的方法求解 I_3：将第一个方程（回路 ABC）乘以 4，将第二个方程（回路 ABD）乘以 10，再相减：

方程 1（×4）：

方程 2（×10）：

方程 2 – 方程 1：

由此得：

根据基尔霍夫节点定律：

流经电阻 R_1 的总电流为：

因此：

有了这些数值，我们便可计算电路中各元件及各节点处的电压降。

本例题二的电路本可仅用欧姆定律简单求解，但我们这里使用基尔霍夫电流定律，以展示在无法直接应用欧姆定律时，如何利用 KCL 求解更复杂的电路。

附录

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。