电流源
Current Sources
电流源是一种有源电路元件,能够在其端子两端的电压如何变化时,向电路提供恒定的电流。
顾名思义,电流源是一种保持恒定电流流动的电路元件,不受端子两端电压的影响——该电压由电路中的其他元件决定。也就是说,理想恒流源会持续提供指定的电流量,而不考虑其驱动的阻抗,因此,理想电流源在理论上可以提供无限的能量。因此,正如电压源可以被额定为例如 5\mathrm{V} 或 10\mathrm{V} 等,电流源也会有电流额定值,例如 3\mathrm{A} 或 15\mathrm{A} 等。
理想恒流源的表示方法与电压源类似,但其符号为一个圆圈,内部带有一个箭头,用于指示电流的流动方向。电流的流动方向与相应电压的极性相对应,从正端流出。字母“i”用于表示电流源,如下所示。
理想电流源
Ideal Current Source
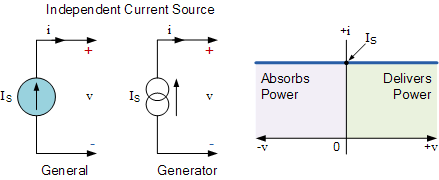
然后,理想电流源被称为“恒流源”,因为它在稳态下提供恒定的电流,与所连接负载无关,其 I\text{-}V 特性曲线是一条直线。与电压源一样,电流源可分为独立源(理想源)或受控源(受电路中其他位置的电压或电流控制),而这些控制量本身可以是恒定的或时变的。
理想独立电流源通常用于电路定理的求解以及包含实际有源元件的电路分析技术。电流源最简单的形式是将一个电阻与电压源串联,其产生的电流范围可从几毫安(\mathrm{mA})到数百安培(\mathrm{A})不等。请记住,当 R = 0 时,零值电流源等效于开路。
电流源的概念是一个两端元件,箭头指示电流的流动方向。电流源具有一个电流值 i,单位为安培( \mathrm{A}),通常简称为“安”。电流源与网络中电压变量之间的物理关系由欧姆定律给出,因为这些电压和电流变量具有确定的数值。
当在所连接电路中存在其他电压源或电流源时,很难仅根据电流来指定理想电流源的端电压大小和极性。这种情况下,我们可能知道电流源提供的电流,但无法确定其两端电压,除非给出了电流源所提供的功率,即
然而,如果电路中唯一的源就是该电流源,那么确定其两端电压的极性就容易得多。但如果存在多个源,则端电压将取决于电流源所连接的网络。
电流源的连接
Connecting Current Sources Together
与电压源一样,理想电流源也可以相互连接以增加(或减少)可用电流。但对于不同数值的多个独立电流源如何串联或并联,有一套规则。
并联电流源
Current Source in Parallel
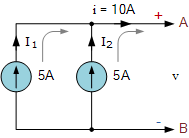
将两个或多个电流源并联,相当于一个电流源,其总电流输出等于各独立电源电流的代数和。在本例中,将两个 5\mathrm{A} 电流源并联,可得到
不同数值的电流源也可并联连接。例如,将一个 5\mathrm{A} 电流源与一个 3\mathrm{A} 电流源并联,由于两者箭头方向相同,电流相加,等效为一个 8\mathrm{A} 电流源。这种连接称为并联增效(parallel-aiding)。
虽然在电路分析中并非最佳实践,但并联抵消(parallel-opposing)连接是将方向相反的电流源并联,其等效电流源的数值等于各电源电流的代数差。
并联抵消电流源
Parallel Opposing Current Sources
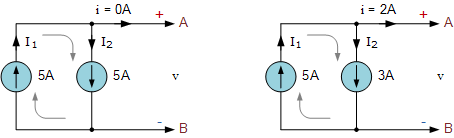
并联抵消电流源 虽然这并非电路分析的最佳实践,但“并联抵消”连接是将方向相反的电流源并联,其等效电流源的数值等于各电源电流的代数差。由于两电流源箭头方向相反,按照基尔霍夫电流定律(KCL),二者相减。例如,两个5\mathrm{A} 电流源并联时,
若电流源分别为 5\mathrm{A} 与 3\mathrm{A},则其等效电流为
我们已经看到理想电流源可以并联形成并联增效或并联抵消连接。不被允许或不推荐用于电路分析的,是将理想电流源进行串联组合。
串联电流源
Current Sources in Series
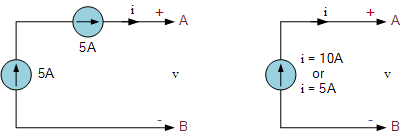
电流源不允许串联连接,无论数值是否相同。在此例中,两个各为 5\mathrm{A} 的电流源被串联连接,但其等效电流应是多少?是等于单个 5\mathrm{A} ,还是等于两者之和 10\mathrm{A}串联连接电流源会为电路分析引入不确定因素,故不宜使用。
另一个不允许串联电流源用于电路分析的原因是,它们可能无法以相同方向提供相同电流。对于理想电流源,不存在“串联增效”或“串联抵消”的概念。
电流源示例 1
两个分别为 250\mathrm{mA} 和 150\mathrm{mA} 的电流源,以并联增效(parallel-aiding)方式连接,为一个 20\Omega 的负载供电。
计算负载两端的电压降;
计算所消耗的功率;
绘制该电路图。
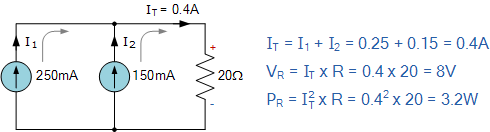
然后,I_T = 0.4\,\mathrm{A} 或 400\,\mathrm{mA}, V_R = 8\,\mathrm{V},以及 P_R = 3.2\,\mathrm{W}。
实际电流源
Practical Current Source
我们已经看到,理想恒流源可以无限期地提供相同的电流,而不考虑其端子两端的电压,因此它是一个独立源。这就意味着电流源具有无限内阻(R = \infty)。这一思想在电路分析中运作良好,但在现实世界中,电流源的行为略有不同,因为实际电流源总是具有内阻,无论多大(通常在兆欧姆量级),导致所产生的电流源随负载而略有变化。
一个实际的或非理想的电流源可以表示为一个并联有内阻的理想电流源。该内阻(R_P)产生的效果等同于与电流源并联(分流)连接的一个电阻。如图所示,并联的电路元件具有相同的电压降。
理想电流源和实际电流源
Ideal and Practical Current Source
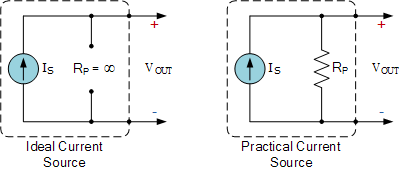
你可能已经注意到,实际电流源与诺顿等效电路非常相似,因为诺顿定理指出:“任何线性直流网络都可等效为一个恒定电流源 I_S 与一个电阻 R_P 并联的电路”。请注意,如果此并联电阻很小, R_P = 0,则电流源被短路;当并联电阻很大或趋于无穷大时, R_P \approx \infty,即可将电流源视为理想源。
理想电流源在 I\text{-}V 特性曲线上绘制为一条水平直线,如前所示。然而,由于实际电流源具有内部源阻,这会分流部分电流,使得其实际特性曲线不再完全水平,而是随着电流分为两部分:一部分流入并联电阻 R_P,另一部分流向输出端子,因而输出电流随端电压变化而略有降低。
欧姆定律告诉我们,当电流 i 流过电阻 R 时,会在该电阻上产生电压降,其数值为
因此,若不接负载,输出电压 V_{\text{OUT}} 即为此电压降。回想理想电流源时,因内部电阻 R_P 为无穷大,不会产生电压降,故端电压为零。
根据基尔霍夫电流定律(KCL),环路电流之和为:
该方程可用于绘制输出电流的 I\text{-}V 特性曲线,其为一条斜率为 -\tfrac{1}{R_P} 的直线,并在理想源情况下与电流轴交于 I_S 点,如图所示。
实际电流源特性
Practical Current Source Characteristics
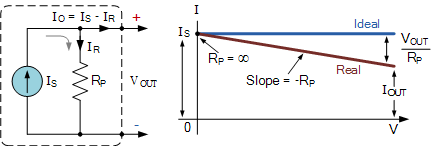
因此,所有理想电流源的 I\text{-}V 特性曲线都是一条直线,但非理想(实际)电流源的 I\text{-}V 特性曲线会略微向下倾斜,其倾斜量等于 \tfrac{V_{\mathrm{OUT}}}{R_{P}},其中 R_{P} 为内部并联源电阻。
教程示例 2
一个实际电流源由一个 3\mathrm{A} 的理想电流源和一个 500\Omega 的内部并联电阻组成。在无负载连接的情况下,计算电流源的开路端子电压以及内部电阻在无负载时吸收的功率。
无负载数值:
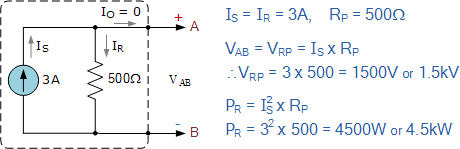
因此,跨过内部源电阻及 A、B 端子的开路电压( V_{AB})计算为:1500 伏(或 1.5 kV)。
第 2 部分:如果在同一实际电流源的 A 和 B 端子之间连接一个 250\Omega 负载电阻,计算流过每个电阻的电流、每个电阻吸收的功率以及负载电阻上的电压降。绘制相应电路。
连接负载时给定的数据: I_{S} = 3\mathrm{A}, R_{P} = 500\Omega 和 R_{L} = 250\Omega。
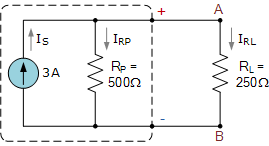
为了求出流经每个电阻分支的电流,我们可以使用电流分配规则。
I_{RP} = \frac{R_{L}}{R_{P} + R_{L}}\times I_{S} = \frac{250}{500 + 250}\times 3 = 1\ \mathrm{A} \\ I_{RL} = \frac{R_{P}}{R_{L} + R_{P}}\times I_{S} = \frac{500}{250 + 500}\times 3 = 2\ \mathrm{A} \\ \therefore\quad I_{RP} + I_{RL} = 1 + 2 = 3\ \mathrm{A} = I_{S}每个电阻吸收的功率如下:
P_{RP} = I_{RP}^{2}\times R_{P} = \bigl(1\,\mathrm{A}\bigr)^{2}\times 500\,\Omega = 500\,\mathrm{W}, \\ P_{RL} = I_{RL}^{2}\times R_{L} = \bigl(2\,\mathrm{A}\bigr)^{2}\times 250\,\Omega = 1000\,\mathrm{W}.然后,负载电阻 R_{L} 上的电压降表示为:
V_{AB} = I_{S} \times R_{T} \\ R_{T} = \frac{R_{P} \times R_{L}}{R_{P} + R_{L}} = \frac{500 \times 250}{500 + 250} = 166.7\,\Omega \\ \therefore\;V_{AB} = 3 \times 166.7 = 500\,\mathrm{V}.我们可以看到,开路情况下的实际电流源端子电压可以非常高——在本例中为了维持规定的电流,会产生所需的 1500\,\mathrm{V}。理论上,当电源试图输出额定电流时,该端子电压可趋于无限大。
在其端子上连接负载会降低电压——在本例中为 500\,\mathrm{V},因为电流现在有路径可走,对于恒流源而言,端子电压与负载电阻成正比。
对于每个都具有内阻的非理想电流源,其总内阻(或阻抗)相当于将这些内阻并联,正如电阻并联时的等效方式。
受控电流源
Dependent Current Source
我们现在知道,理想电流源可提供与其两端电压无关的指定电流量,并会产生维持该电流所必需的任何电压,因此称为理想独立电流源。
而受控(依赖)电流源则会根据电路中其他元件上的电压或电流变化而改变其输出电流。换言之,受控电流源的输出由另一电压或电流信号控制。
受控电流源的行为与我们之前见过的理想(独立)电流源和实际电流源类似,区别在于它们可由输入电压或输入电流控制。依赖电压输入的电流源通常称为电压控制电流源(Voltage Controlled Current Source,VCCS);依赖电流输入的电流源通常称为电流控制电流源(Current Controlled Current Source,CCCS)。
通常,理想受控电流源(无论 VCCS 还是 CCCS)都用一个菱形符号表示,箭头指示电流方向 i,如下所示。
受控电流源符号
Dependent Current Source Symbols

理想受控电压控制电流源(VCCS)保持输出电流 I_{\mathrm{OUT}} 与控制输入电压 V_{\mathrm{IN}} 成正比。换言之,输出电流“依赖”于输入电压的数值,使其成为一种受控电流源。
VCCS 的输出电流由下式给出:
乘数常数 \alpha 的国际单位制单位为摩(mho),符号 ℧(倒欧姆符号),因为
其单位即为安培/伏特。
理想受控电流控制电流源(CCCS)保持输出电流与控制输入电流成正比。输出电流“依赖”于输入电流的数值,再次成为一种受控电流源。
作为控制电流, I_{\mathrm{IN}} 决定放大系数 \beta 作用下的输出电流 I_{\mathrm{OUT}},CCCS 元件的输出电流由下式确定:
注意,乘数常数 \beta 是无量纲的缩放因子,因为
其单位为安培/安培。
教程总结
我们在本教程中看到了,理想电流源(R = \infty)是一种有源元件,可提供与其两端电压无关的恒定电流,其 I\text{-}V 特性表现为一条直线。
理想独立电流源可并联连接,用于电路分析技术,既可形成并联增效,也可形成并联抵消,但不可串联。同时,在求解电路定理时,电流源可视作开路源使其电流为零。注意,电流源既能输出功率,也能吸收功率。
对于非理想或实际电流源,可等效为并联有内部电阻的理想电流源,该内阻虽不为无穷大但值极高(R \approx \infty),因此其 I\text{-}V 特性不再水平,而是随着负载减小略微向下倾斜。
我们还看到,电流源可分为独立源和受控源。受控源的数值取决于其他电路变量。电压控制电流源(VCCS)和电流控制电流源(CCCS)即为受控电流源的两种类型。
具有极高内阻的恒流源在电子电路与分析中应用广泛,可采用双极晶体管、二极管、稳压二极管、场效应晶体管及这些固态器件的组合来实现。
附录
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

