相量图与相量代数

Phasor Diagrams and Phasor Algebra

相量图是一种图形化表示方法，用于表示两个或多个交流量之间的幅值及其方向关系。

相量图是在坐标系中绘制的一种图形化表示，用于描述被动元件或整个电路中电压与电流之间的相位关系。通常，相量都是相对于某一参考相量来定义的，该参考相量始终沿 x 轴正方向指向右方。

相同频率的正弦波形之间可以存在相位差，用以表示两个正弦波形之间的角度差异；术语“超前”“滞后”以及“同相”“反相”也常用来说明一个波形相对于另一个波形的关系。广义的正弦波时域表达式为：

但以这种数学形式呈现时，有时难以直观地看出两个或多个正弦波形之间的角度（相量）差异。为了解决这一问题，可以使用相量图Phasor Diagrams在空间域（或称相量域）spacial or phasor-domain中以图形方式表示正弦波，这正是旋转矢量法的核心。

旋转矢量rotating vector（也称“相量矢量”Phase Vector）本质上是一条经过缩放的线段，其长度表示交流量的幅值（峰值），其方向表示该量的相位，并且这条线段在某一时刻被冻结下来，便于在图中比较不同波形的相位关系。

一个在一端带有箭头的矢量，这个箭头既表示该矢量量（ V_m 或 I_m）的最大值，也表示矢量旋转的端点。

通常，矢量被假定为在其一端绕一个固定的零点——称为“原点”——进行枢轴旋转。带箭头的一端代表可以以角速度 \omega 逆时针自由旋转的量。逆时针旋转被视为正方向，顺时针旋转则被视为负方向。

虽然“矢量”（vector）和“相量”（phasor）这两个术语都用来描述既有大小又有方向的旋转线，但二者的主要区别在于：

• 矢量的大小表示正弦波的“峰值”（peak value），

• 相量的复数幅值表示正弦波的“有效值”（rms value），因为相量主要用于含有电抗reactance的交流电路。

在这两种表示中，相位角、方向和角速度都相同。

在任一时刻，交流量的相位都可以用相量图来表示，因此相量图可以看作是“时间函数”的图示。一个完整的正弦波可以由一个以角速度 \omega = 2\pi f（其中 f 为波形频率）逆时针旋转的矢量构成。相量，即同时具有“大小”和“方向”的量。

此外，矢量遵循平行四边形加法与减法法则，可以相加得到一个以相同角速度逆时针旋转的合矢量。而相量则更多地以数学形式出现：矩形形式、极坐标形式或指数形式，例如 a + j b。相量表示法定义了电压和电流的有效（rms）幅值。

在构建相量图时，通常假定正弦波的角速度 \omega 的单位为弧度每秒（rad/s）。请参见下面的相量图示例。

正弦波的相量图

Phasor Diagrams for a Sinusoidal Waveform

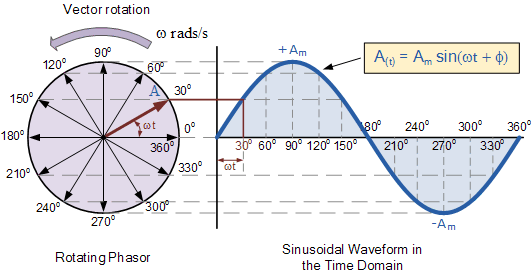
随着单一矢量以逆时针方向旋转，其在点 A 处的尖端将完成 360° 或 2\pi 的一整圈，代表一个完整周期。

如果将该尖端在不同时刻对应的不同角度投影到如上图所示的坐标图中，就会从左侧的零时刻 t = 0 开始绘出正弦波形。水平轴上的每一点均表示自零时刻起经过的时间。当矢量水平时，尖端对应的角度为 0°、180° 和 360°。

同样，当尖端垂直时，它分别表示 90° 或 \frac{\pi}{2} 处的正峰值（+Aₘ）和 270° 或 \frac{3\pi}{2} 处的负峰值（−Aₘ）。此时波形的时间轴即表示相量已旋转的角度（以度或弧度计）。因此，我们可将相量视为在某一时刻 t “冻结”下来的旋转矢量所对应的缩放电压或电流值，在本例中该冻结角度为 30°。

在分析交流波形时，常需要确定相量在某一特定时刻的位置，尤其是在将两种不同波形（如电压和电流）在同一坐标上进行比较时。上图中假设波形在 t = 0 时开始，对应某一相位角（以度或弧度表示）。

但如果第二个波形相对于零点向左或向右偏移，或者我们希望在相量表示法中表达两个波形之间的关系，就必须考虑该波形的相位差 Φ。请参见前一节“相位差”教程中的示意图。

正弦波的相位差

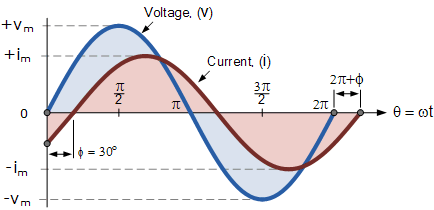
定义这两个正弦量的广义数学表达式可写为：

其中，

• V_m 和 I_m 分别是电压和电流的峰值，

• \omega 是角频率，

• \phi 是电压与电流之间的相位差。

电流 i 相对于电压 v 滞后角度 \Phi，在上例中 \Phi = 30^\circ。因此，表示这两种正弦量的两个相量之间的夹角就是 \Phi，所得到的相量图如下：

正弦波的相量图

Phasor Diagram of a Sinusoidal Waveform

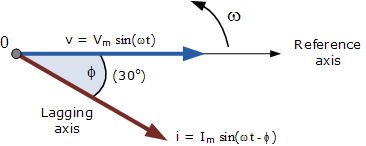
相量图是在水平轴对应零时刻（ t = 0）时绘制的。相量的长度与在该瞬时刻的电压（V）和电流（I）值成正比。

如前所述，电流相量相对于电压相量以角度 \Phi滞后，因为两者都以逆时针方向旋转，因此该角度 \Phi 也是以相同的逆时针方向来测量的。

30° 时的相量图

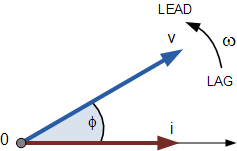
如果在 t = 30° 处冻结波形，对应的相量图如上图所示。此时，电流相量仍然滞后于电压相量，因为两者频率相同。

然而，由于此刻电流波形正在穿过水平零轴线，我们可以将电流相量作为新的参考，相应地说电压相量相对于电流相量“超前”角度 \Phi。无论哪种情况，都要将其中一个相量指定为参考，其他所有相量则相对于该参考表现为超前或滞后。

相量图的相量相加

相量的一个重要应用是对同频率正弦波的叠加。在研究正弦波时，有时需要将两个不“同相”的交流波形（例如在交流串联电路中）进行相加。

• 如果它们“同相”（即没有相位差），则可像直流量一样直接代数相加，得到两个矢量的代数和。例如，若两电压分别为 50 V 和 25 V 且同相，则它们相加后得到一个 75 V 的电压（50 + 25）。

• 如果它们不同相（即方向或起始点不一致），就必须考虑它们之间的相位角，利用相量图并应用平行四边形法则，来确定它们的合成相量（结果相量或矢量和）。

例子 设有两交流电压：

• V_1 的峰值为 20 V，

• V_2 的峰值为 30 V，且 V_1 超前 V_2 \ 60^\circ。

要计算二者的总电压 V_T，首先画出表示这两个矢量的相量图，然后以 V_1 和 V_2 为两条邻边构造一个平行四边形，如下图所示。

两个相位相加

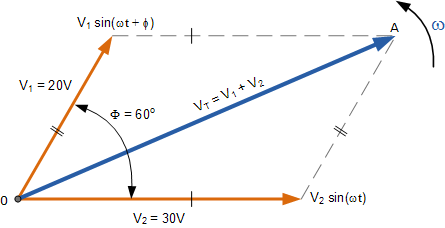
通过在方格纸上按比例绘出两个相量，可以通过测量从原点到构造线 0–A 交点的对角线——称为“结果 r 矢量”——的长度，轻松地求得它们的相量和 V_1 + V_2。这种图解法的缺点是按比例绘制相量非常耗时。

此外，虽然该图解法对于大多数用途而言已经足够准确，但如果绘制不够精确或比例不正确，可能会产生误差。为确保始终得到正确结果，可以采用分析法。

在数学上，我们可以先确定两个电压的“垂直”与“水平”方向，然后据此计算结果“r 矢量” V_T 的“垂直”与“水平”分量。这种使用余弦定理和正弦定理来求得结果值的分析方法，通常称为矩形形式（Rectangular Form）。

在矩形形式中，相量被分解为实部 x 和虚部 y，形成广义表达式 Z = x \pm j y（我们将在下一个教程中对此做更详细的讨论。）这样就得到一个既表示正弦电压幅值又表示其相位的数学表达式：

复数正弦量的定义

因此，使用上述广义表达式，两个向量 A 和 B 的相加如下：

矩形形式下的相量相加

电压 V_2 = 30\,\mathrm{V} 指向水平零度参考方向，因此只有水平分量，没有垂直分量：

• 水平分量： 30\cos0^\circ = 30\,\mathrm{V}

• 垂直分量： 30\sin0^\circ = 0\,\mathrm{V}

由此可得

电压 V_1 = 20\,\mathrm{V} 相对于 V_2 超前 60^\circ，因此既有水平分量也有垂直分量：

• 水平分量： 20\cos60^\circ = 20\times0.5 = 10\,\mathrm{V}

• 垂直分量： 20\sin60^\circ = 20\times0.866 = 17.32\,\mathrm{V}

由此可得

合成电压 V_T 的水平和垂直分量分别为：

• V_1和 V_2的实数部分real parts相加

• V_1和 V_2的虚数部分image parts相加

确定了水平分量和垂直分量后，即可用直角三角形的勾股定理计算合成电压幅值：

然后所得的相量图为：

V_t 的合成值

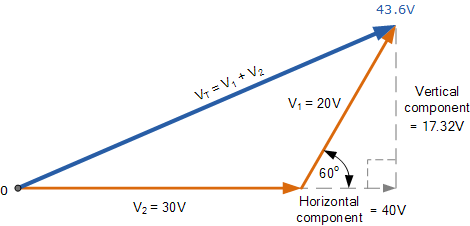
相量图的相量减法

相量减法与上述矩形形式的相量加法非常相似，只不过这一次要求的是由 V_1 和 V_2 两个电压构成的平行四边形的另一条对角线——即两相量之差，如下图所示。

两个相量的矢量减法

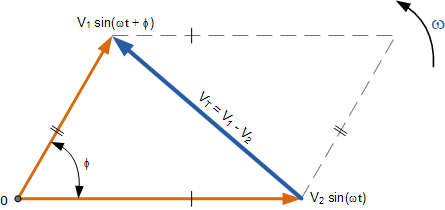
这一次，我们不是将水平分量和垂直分量相加，而是将它们相减。

三相相量图

The 3-Phase Phasor Diagrams

之前我们只研究了在磁场中旋转的单相多匝线圈所产生的交流波形。但如果在同一转子轴上放置三个相同匝数的线圈，并且它们在电角度上彼此相差 120°，就能产生三相电压。

平衡三相电压由三组幅值和频率完全相同、但相互之间相位相差 120° 的正弦电压组成。

标准做法是用红、黄、蓝三种颜色标识三相，其中红相（R）作为参考相。

三相电源的正常旋转顺序为红 → 黄 → 蓝（R → Y → B）。

与上述单相相量一样，三相系统的相量也绕中心点以ω（rad/s）所示方向逆时针旋转。下图分别给出了平衡 Y （星形star）和 Δ （三角形delta ）连接系统的三相相量图。

三相相量图

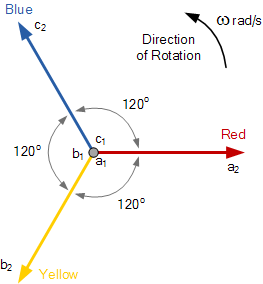
相电压幅值相等，仅在相位角上互相错开。三组绕组在 a_1、b_1 和 c_1 点汇合，形成三相电源的公共中性点common neutral。若以红相为参考相，则各相电压相对于公共中性点可定义为：

三相电压方程

红相：

黄相：

蓝相：

如果如前所述将红相电压 V_{RN} 作为参考电压，则相序为 R–Y–B，黄相电压相对于 V_{RN} 滞后 120°，蓝相电压相对于 V_{YN} 也滞后 120°。但也可以说蓝相电压 V_{BN} 相对于红相电压 V_{RN} 超前 120°。

关于三相系统的最后一点：由于三组正弦电压之间相互固定相差 120°，因此称为“平衡”。在一组三相平衡电压中，它们的相量和始终为零，即：

实部：

\cos0^\circ + \cos120^\circ + \cos240^\circ = 1 - \tfrac12 - \tfrac12 = 0

虚部：

\sin0^\circ + \sin120^\circ + \sin240^\circ = 0 + \tfrac{\sqrt3}{2} - \tfrac{\sqrt3}{2} = 0

所以最终的电压相量实部+虚部=0

相量图总结

• 简而言之，相量图是将旋转矢量投影到表示瞬时值的水平轴上。由于相量图可用于任何时刻和任何角度，因此交流量的参考相量始终沿 x 轴正方向绘制。

• 矢量、相量与相量图仅适用于正弦交流量。

• 相量图可表示任一时刻的两个或多个正弦交流量。

• 通常先将参考相量绘制在水平零轴上，然后在同一时刻绘出其他相量，所有相量均以此零轴为参照。

• 相量图可用于多于两个的正弦波，它们可以是电压、电流或其他交流量，但频率必须相同。

• 所有相量都沿逆时针方向旋转。位于参考相量前方的相量称“超前”，后方的称“滞后”。

• 相量的长度一般表示该正弦量的有效值（r.m.s），而非峰值。

• 不同频率的正弦波由于矢量转速不同，无法在同一相量图中表示；任一时刻它们之间的相位角也因此各异。

• 多个矢量可通过相量加减合成为一个“合成矢量”。

• 矢量的水平分量对应实部（x 分量），垂直分量对应虚部（y 分量）；直角三角形的斜边即为 r 分量。

• 在平衡三相系统中，每个相量彼此相位相差 120°。

• 下一个教程中，将介绍如何以复数的矩形形式、极坐标形式和指数形式来表示正弦波形。

附录

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。