交流波形和交流电路理论

AC Waveform and AC Circuit Theory

交流正弦波形是通过在磁场中旋转线圈产生的，交流电压和电流构成了交流理论的基础

电路理论中最常用的交流波形是正弦波。电压源形式的周期性交流波形会产生电动势 (EMF)，其极性会定期反转，完成一次完全反转所需的时间称为波形周期。

直流电波形

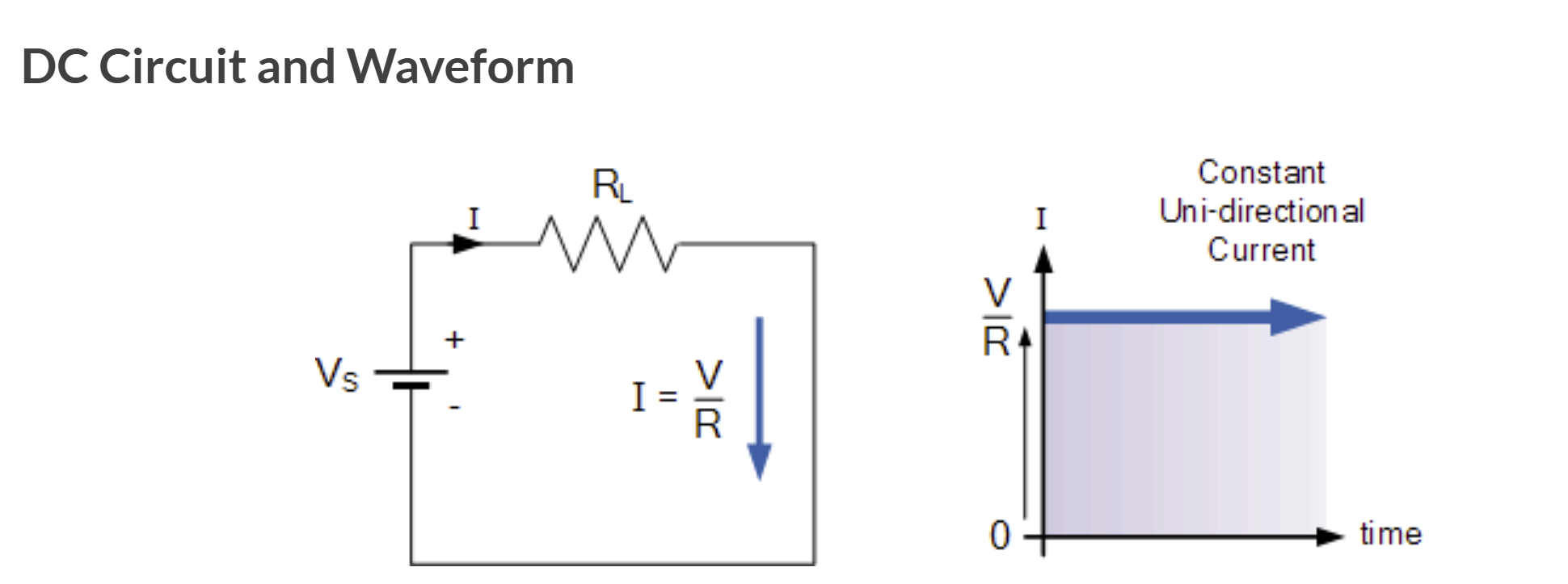
直流电或通常所说的 DC 是一种电流或电压，它仅在一个方向上在电路中流动，使其成为“单向”Uni-directional电源。

通常，直流电流和电压都由电源、电池、发电机和太阳能电池等产生。直流电压或电流具有固定的幅值（振幅）和明确的方向。例如， +12V 表示正向 12伏， -5V 表示负向 5 伏。

我们还知道，直流电源的电流值不会随时间变化，而是沿连续稳定方向流动的恒定值。换句话说，直流电始终保持相同的值，而恒定的单向直流电源永远不会改变或变为负值，除非其连接发生物理反转。下图显示了一个简单的直流或直流电路示例。

交流电波形

另一方面，交流波形描述其幅度和极性随时间的周期性变化，通常可表示为：

其中：

• A_{max}：峰值幅度（Peak）；

• f：频率（Hz），表示每秒振动次数；

• t：时间（s）；

• \phi：初相位（rad），决定波形在 t=0 时的相位。

术语 AC 或交流电（Alternating Current） 指随时间周期性变化的电压或电流波形，其中最常见的形式是正弦波。

正弦波形通常简称为正弦波 。正弦波是迄今为止电气工程中使用的最重要的交流波形类型之一。

绘制电压或电流的瞬时纵坐标值随时间变化的形状称为交流波形 。交流波形每半个周期不断改变其极性，分别在正最大值和负最大值之间随时间交替变化，一个常见的例子是我们在家中使用的家用电源电压。

这意味着交流波形是一种时间相关信号，其中最常见的时间相关信号类型是周期波形 。周期波形或交流波形是旋转发电机的产物。

交流波形与旋转发电机

当导体线圈在恒定磁场中以匀速角速度 ω 旋转时，穿过线圈的磁通量 Φ 会按余弦函数规律变化：

Φ(t)=Φ_{max}cos(ωt)

根据法拉第电磁感应定律，线圈两端感应电动势为磁通变化率的负值：

e(t)=−\frac{dΦ}{dt}=ωΦ_{max}sin(ωt)

这正是一条峰值为 ωΦ_{max}的正弦波

简而言之：

1. 磁通变化：线圈旋转导致磁通周期性增减；

2. 电磁感应：磁通变化速率生成感应电动势；

3. 正弦特性：由于磁通本身是余弦函数，其导数自然是正弦函数。

通常，可以使用基频并将其与不同频率和幅度的谐波信号叠加来生成任何周期波形的形状，但这是另一个教程的内容。

交流电压和电流不能像直流电 (DC) 那样存储在电池或电池单元中，在需要时使用交流发电机或波形发生器来产生这些量要容易得多，也便宜得多。

交流波形的类型和形状取决于产生它们的发生器或设备，但所有交流波形都由一条零电压线a zero voltage line（坐标轴）组成，该零电压线将波形分成两个对称的部分。交流波形的主要特征定义为：

• 周期 (T) 是波形从开始到结束重复所需的时间长度，以秒为单位。

  对于正弦波，也可以称为波形的周期时间 ；对于方波，也可以称为脉冲宽度 （数字信号）。

• 频率 (ƒ) 是波形在一秒钟内重复的次数。频率是时间周期的倒数 ( ƒ = 1/T )，频率单位是赫兹(Hz)。

• 振幅 (A) 是以伏特或安培为单位测量的信号波形的大小或强度。

在我们的波形教程中，我们研究了不同类型的波形，并说“波形基本上是以时间为基准绘制的电压或电流变化的视觉表示”。

一般来说，对于交流波形来说，这条水平基线代表电压或电流的零点状态。交流波形中位于水平零轴上方的任何部分都表示电压或电流沿一个方向流动。

同样，波形中位于水平零轴以下的任何部分都表示与第一个零轴方向相反的电压或电流。通常，对于正弦交流波形，零轴上方的波形形状与其下方的形状相同。然而，对于大多数非功率交流信号（包括音频波形）而言，情况并非总是如此。

其他波形

电气和电子工程中最常用的周期信号波形是正弦波形。然而，交流电波形并不总是基于三角正弦或余弦函数的平滑形状。交流电波形也可以采用复杂波、方波或三角波的形状，如下所示。

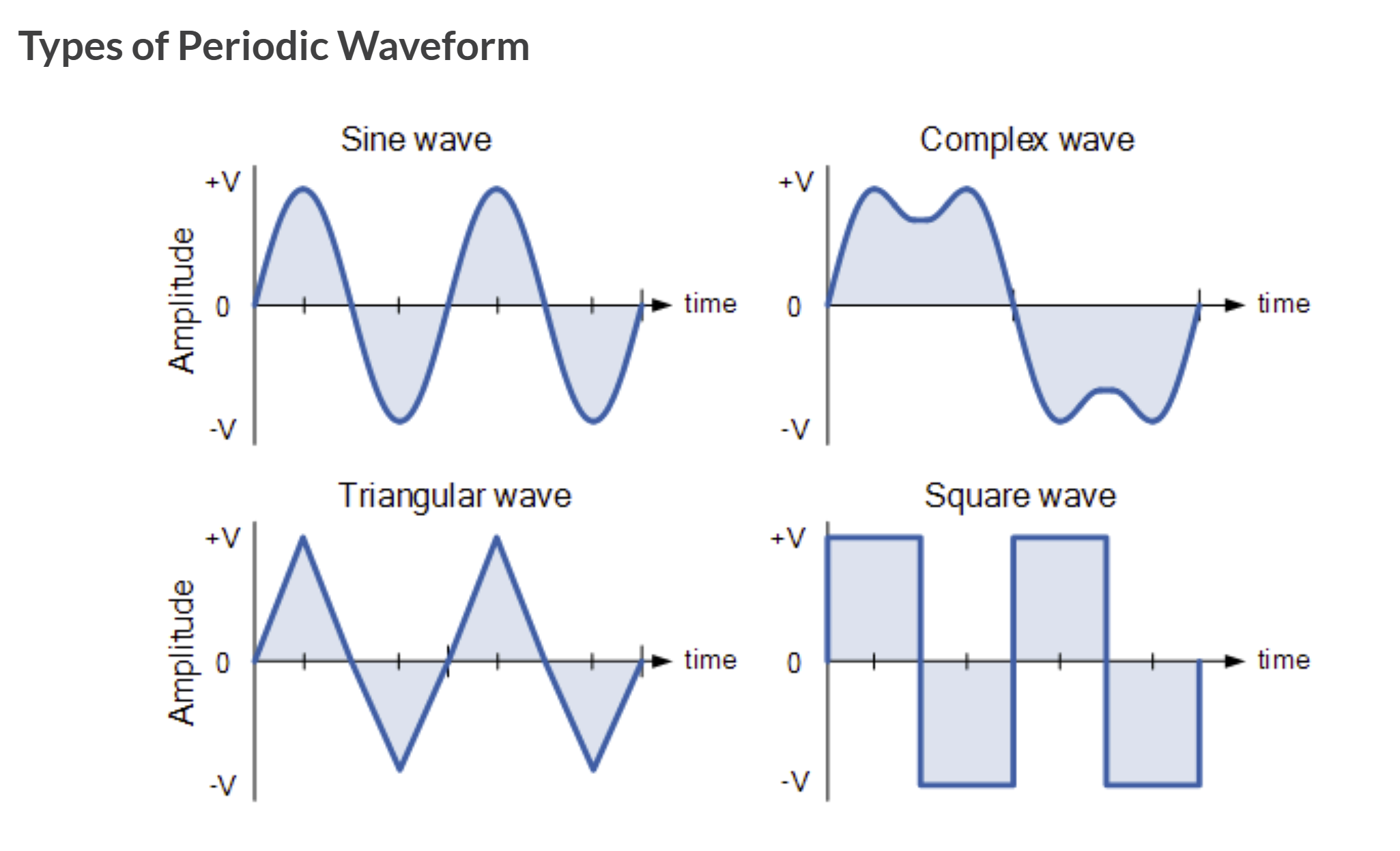
交流波形从正半周开始，经过负半周再回到零基线所需的时间称为一个周期（Cycle），一个完整的周期包含正半周和负半周。波形完成一个完整周期所需的时间称为周期时间（Periodic Time），用符号 T 表示。

在一秒钟内完成的完整周期数（周期/秒）称为频率（Frequency），用符号 f 表示。频率的单位是赫兹（Hz），以德国物理学家海因里希·赫兹命名。

由此可见，周期（振荡次数）、周期时间与频率（每秒周期数）之间存在如下关系：如果在一秒钟内有 f 个周期，则每个周期所需的时间必定为T = \frac{1}{f}

周期和频率的关系

f=\frac{1}{T}\;,\quad T=\frac{1}{f} \\ f=\frac{1}{T}\;[\mathrm{Hz}],\quad T=\frac{1}{f}\;[\mathrm{s}]

交流波形示例 1

1. 周期时间 (T) 对于 50 Hz 的正弦波，

   T = \frac{1}{f} = \frac{1}{50} = 0.02\ \text{s} = 20\ \text{ms}

2. 频率 (f) 若波形的周期时间为 10 ms，则

   f = \frac{1}{T} = \frac{1}{10\times10^{-3}} = 100\ \text{Hz}

频率过去常用“每秒周期数”（cycles per second，简称 cps）来表示，而现在一般用“赫兹”（Hertz, Hz）作为单位。在各国的市电系统中，电网频率通常为 50 Hz 或 60 Hz，由发电机的转速决定。由于 1 Hz 较小，对更高频率的波形常使用千赫（kHz）、兆赫（MHz）甚至吉赫（GHz）等单位前缀。

频率前缀定义

交流波幅值

除了已知交流量的周期时间或频率外，交流波形的另一个重要参数是幅值Amplitude，亦称最大值或峰值，通常用 V_{\max} 表示电压峰值，I_{\max} 表示电流峰值。

峰值是指波形在每个半周期中从零基线出发所能达到的最大电压或电流值。与可用欧姆定律计算或测量的直流电压／电流不同，交流量的瞬时值会随着时间不断变化。

对于纯正弦波，其正负峰值大小相等：

但对于非正弦或复杂波形，各半周期的最大峰值可能并不相同，需分别测量。

有时也用峰–峰值（peak-to-peak，记作 V_{p\!-\!p}）来描述交流波形，它等于正峰值与负峰值之间的电压差：

对于非对称波形，峰–峰值仍按正峰与负峰之差定义，但需分别取各自的最大和最小峰值。

交流波的均值

连续直流电压的平均值始终等于其最大峰值，因为直流电压在时间上保持恒定。只有当直流电压的占空比发生变化时，这个平均值才会随之改变。对于纯正弦波，如果在整个周期内计算平均值，结果将等于零——因为正半周与负半周相互抵消。因此，交流波形的平均值或算术平均通常只在半个周期内计算或测量，如下所示。

非正弦波的均值

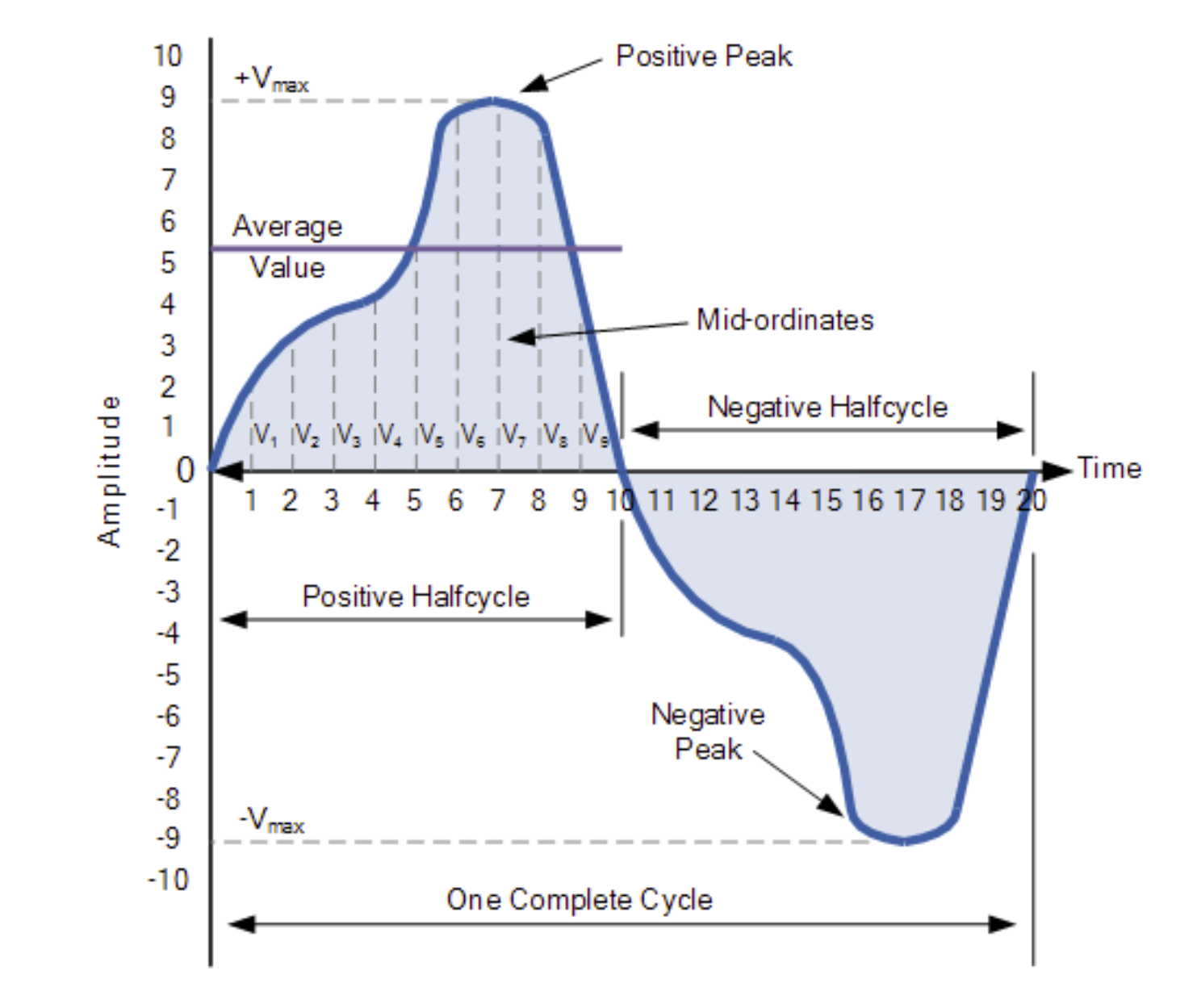
要计算波形的平均值，需要用数学中常见的中点法、梯形法或辛普森法来求出波形下方的面积。对于任意不规则波形，使用中点法就能快速近似求得其下面积。

首先，将零电压基线等分成若干段，在上面示例中我们一共划出了九段（对应各点 V_1 到 V_9）。划分的分段越多，得到的平均值或算术平均就越准确。平均值即是将所有这些瞬时取样值相加，再除以取样点的总数，计算公式为：

交流波均值

其中：n 为实际使用的中点数。

对于纯正弦波，该平均值始终等于 0.637\times V_{\max}，该关系同样适用于电流的平均值。

交流波形的均方根值（RMS）

交流波形的有效值（RMS）

我们上面计算出的交流波形平均值（即 0.637\times V_{\max}）并不能直接用于等效直流电源的电压。这是因为，与恒定不变的直流电源不同，交流波形的瞬时值在不断变化，没有固定的数值。为了得到一个与直流电路提供相同电功率（即在相同负载上产生相同 I^2R 发热效应）的交流电压或电流值，引入了“有效值”这一概念。

对于正弦波，其有效值（也称为均方根值，Root Mean Squared，RMS）定义为：

各个瞬时取样值的平方的平均值，再开平方。

记作 V_{rms} 或 I_{rms}，它等价于一个恒定的直流量，该直流量在相同负载上产生与该交流波形相同的发热功率。

任何交流波形的 RMS 值，都可以通过如下形式的“修正平均值”公式来计算：

交流波形的均方根（RMS）值

其中：n 为所用中点（mid-ordinate）个数。

• 对于纯正弦波，其有效值（RMS）恒等于峰值的 \tfrac{1}{\sqrt2} 倍，即

  V_{\mathrm{RMS}} = \frac{V_{\max}}{\sqrt2} \approx 0.707\,V_{\max},

  同样适用于电流的 RMS 值。

• 正弦波的 RMS 值一般大于其平均值；仅在矩形波（方波）情况下，因加热效应恒定，平均值与 RMS 值才相等。

关于测量： 大多数数字或模拟万用表（除非另有说明）默认测量电压和电流的 RMS 值，而非平均值。因此：

• 测量直流系统时，读数为

  I = \frac{V}{R};

• 测量交流系统时，读数为

  I_{\mathrm{RMS}} = \frac{V_{\mathrm{RMS}}}{R}

注意： 除非用于平均功率计算，否则在计算 RMS 值或峰值时，应使用 V_{\mathrm{RMS}} 来求 I_{\mathrm{RMS}}，或使用峰值 V_p 来求峰值电流 I_p。切勿将平均值、RMS 值与峰值混用，否则结果必定不正确。

波形因数（Form Factor）与峰值因数（Crest Factor）

尽管如今应用较少，波形因数和峰值因数都可用来反映交流波形的实际形状。波形因数定义为平均值与RMS值之比，表示为：

对于纯正弦波形，波形因数始终等于 1.11。

峰值因数是波形均方根值与峰值之比，定义如下：

对于纯正弦波形，峰值因数始终等于 1.414。

交流波形示例 2

1. 一个 6 安培的正弦交流电流流经一个 40 Ω 的电阻。

2. 计算该电源的平均电压和峰值电压。

有效值电压（RMS）计算如下：

平均电压计算如下：

峰值电压计算如下：

平均值、RMS、波形因数和峰值因数的计算方法也可用于任何类型的周期波形，包括三角波、方波、锯齿波或任何其他不规则或复杂的电压/电流波形。不同正弦波参数之间的换算有时会令人困惑，因此下表提供了一种便捷的正弦波参数相互转换的方法。

交流波形的平均值、RMS 值、波形因数和峰值因数的计算方法同样适用于任何类型的周期波形，包括三角波、方波、锯齿波或任何其他不规则或复杂的电压/电流波形。不同正弦波参数之间的换算有时令人困惑，下面的表格提供了从一种正弦波参数到另一种参数的便捷转换方法。

正弦波参数换算表

在下一节关于正弦波的教程中，我们将介绍正弦交流波形（sinusoid）的产生原理及其角速度表示法。

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。