Transformer 基础知识
Transformer Basics
变压器是一种电气设备,由两个或多个线圈组成,通过变化的磁场来传递电能。
在本变压器基础教程中,我们将看到变压器内部没有任何运动部件,通常用于需要通过电磁感应将电能从一个电路传递到另一个电路时改变电压的场合。
我们在家庭和工作场所使用交流(AC)电压与电流的主要原因之一,是因为交流电源可以在一个合适的电压下容易地生成,并通过变压(因此得名“变压器”)成更高的电压,然后利用国家电网中的输电塔和导线在很长距离上分配。
将电压升高到更高水平的原因在于,对于相同功率而言,更高的输电电压意味着更低的电流,从而沿电网电缆的 I^2R 损耗更小。然后,这些较高的交流输电电压和电流可以再被降低到更低、更安全且可用的电压水平,以为我们家庭和工作场所的电气设备供电。所有这些都归功于电压变压器的基本工作原理。
电压变压器可被视为一种电气元件,而不是电子元件。变压器本质上是一种非常简单的静态(或固定)电磁无源电气装置,它通过法拉第电磁感应定律将电能从一种数值转换为另一种数值。
变压器通过其自身产生的公共振荡磁路,将两个或多个电路连接在一起。变压器的基本工作原理是“电磁感应”,具体形式为互感(Mutual Induction)。
互感是指一组线圈在接近另一组线圈时,通过磁耦合使另一线圈感应出电压的过程。因此,我们可以说变压器工作在“磁场域”中,其名称来源于它能将一种电压或电流水平“变换”为另一种电压或电流水平。
变压器能够在不改变频率或传输功率大小的情况下,提高或降低其输入电压和电流水平。
单相电压变压器基本由两个电气线圈组成,一个称为“一次绕组”Primary Winding,另一个称为“二次绕组”Secondary Winding。在本教程中,我们将“一次侧”primary side定义为通常吸收电能的一侧,将“二次侧”secondary side定义为通常输出电能的一侧。在单相电压变压器中,一次侧通常具有更高的电压。
这两个线圈彼此电气隔离,而是绕制在一个称为“铁芯”的公共闭合磁路上。该软铁芯不是实心的,而是由多个单片层叠而成,以帮助减少铁芯的磁损耗。
一次绕组和二次绕组电气上相互隔离,但通过公共铁芯进行磁耦合,使电能能够从一个线圈传递到另一个线圈。当电流通过一次绕组时,会产生磁场,从而在二次绕组中感应出电压。下图展示了这一变压器基本工作原理。
单相电压变压器
Single Phase Voltage Transformer
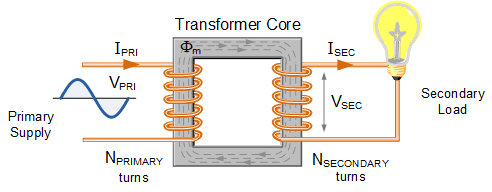
换句话说,对于变压器而言,两组绕组之间没有直接的电气连接,因此又称为隔离变压器Isolation Transformer。通常,变压器的一次绕组连接到输入电压电源,并将电能转换为磁场;而二次绕组的任务是将交变磁场转换为电能,产生所需的输出电压,如下所示。
变压器结构(单相)
Transformer Construction (single-phase)
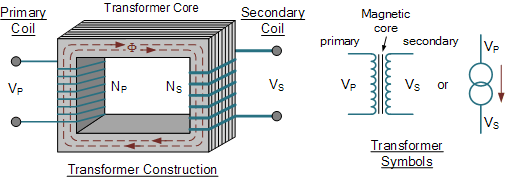
其中:
V_P —— 一次侧电压
V_S —— 二次侧电压
N_P —— 一次绕组匝数
N_S —— 二次绕组匝数
\Phi —— 耦合绕组的磁通
注意,两组绕组之间没有电气连接,仅通过磁场耦合。单相变压器既可用于升高也可用于降低作用于一次绕组的电压。
当变压器用于使二次绕组电压相对于一次绕组电压“升高”时,称为升压变压器(Step-up Transformer)。当用于使二次绕组电压相对于一次绕组电压“降低”时,称为降压变压器(Step-down Transformer)。
然而,还存在第三种情况:变压器在二次侧产生的电压与加在一次侧的电压相同。换言之,其在电压、电流和传输功率方面的输出均与一次侧一致。这种变压器称为“阻抗变压器”(Impedance Transformer),主要用于阻抗匹配或相邻电路的隔离。
一次侧与二次侧绕组电压之差是通过改变一次绕组匝数 N_P 与二次绕组匝数 N_S 之比来实现的。
由于变压器本质上是线性装置,一次绕组匝数与二次绕组匝数之比——即变压器的变比,通常称为匝比(Turns Ratio,TR)——决定了变压器的工作状态及二次侧所能获得的电压。
需要知道一次绕组与二次绕组的匝数之比。匝比是无量纲的,用冒号表示,例如 3:1。
这意味着在此例中,若一次绕组电压为 3 V,则二次绕组电压为 1 V,即 3 比 1。由此可见,当绕组匝数比改变时,输出电压也将按相同比例变化。
变压器的一切运作都与“比值”相关:一次侧与二次侧的匝数比、输入与输出的电压比,以及任何变压器的匝比均等同于其电压比。换言之:
绕组的实际匝数通常并不重要,关键在于匝比,其关系可表示为:
A Transformers Turns Ratio
假设理想变压器且相位角:
注意,当表示变压器匝比时,数字的顺序非常重要,因为匝比 3︰1 所对应的变压器关系和输出电压,与匝比 1︰3 完全不同。
变压器基础 示例 1
一个电压变压器的一次绕组上有 1500 匝线,二次绕组上有 500 匝线。该变压器的匝比(TR)是多少?
这个 3:1(3 比 1)的匝比仅表示每 3 匝一次绕组对应 1 匝二次绕组。当比值从左侧的大数字变为右侧的小数字时,一次侧电压就按此比例被降压,如图所示。
变压器基础 示例 2
如果在上述同一变压器的一次绕组上施加 240\mathrm{V_{rms}},则其空载二次绕组电压为多少?
再次确认该变压器为“降压变压器”,因为一次侧电压为 240\mathrm{V},对应的二次侧电压较低,为 80\mathrm{V}。
那么,变压器的主要作用就是以预定的变比来变换电压,我们可以看到一次绕组上的线圈匝数是根据输入电压预先确定好的。
如果二次输出电压要与一次绕组的输入电压相同,则必须在二次铁芯上绕制与一次铁芯相同匝数的线圈,从而获得匝比为 1:1(一比一)。换句话说,二次侧每一匝对应一次侧每一匝。
如果二次输出电压要高于一次侧输入电压(升压变压器),则二次绕组的匝数必须更多,匝比为 1:N,其中 N 表示匝比数值。同样地,如果二次输出电压要低于一次侧(降压变压器),则二次绕组的匝数必须更少,匝比为 N:1( N 比 1)。
变压器作用
Transformer Action
我们已经看到,二次绕组相对于一次绕组的匝数之比(匝比)会影响二次线圈可获得的电压。但如果两组绕组在电气上彼此隔离,这个二次电压又是如何产生的呢?
前面我们提到,变压器基本上由绕制在同一软铁芯上的两个线圈组成。当在一次线圈上施加交流电压 \,V_P\, 时,电流流经该线圈,进而在其周围建立起磁场。根据法拉第电磁感应定律,这种效应称为互感(mutual inductance)。
当电流从零上升到其最大值时,磁场强度随之增强,其变化率由
给出。

当该电磁体产生的磁力线由线圈向外扩展时,软铁芯为磁通提供了一条通路并将其集中。在交流电源的作用下,此磁通以相反方向增减,并与一次、二次绕组的各匝相互耦合。
然而,注入软铁芯的磁场强度取决于电流大小和绕组匝数。当电流减小时,磁场强度也随之减弱。
当磁力线环绕铁芯流动时,会穿过二次绕组的匝,从而在二次线圈中感应出电压。感应电压的大小由法拉第电磁感应定律决定:
其中 N 为线圈匝数。此外,该感应电压与一次绕组电压具有相同的频率。
由此可见,由于相同的磁通同时耦合到两组绕组的每一匝上,因此两绕组的每一匝都会感应出相同的电压。结果,每个绕组的总感应电压与该绕组的匝数成正比。但若铁芯的磁损耗较大,二次侧输出电压的峰值幅度则会有所降低。
如果我们希望一次绕组产生更强的磁场以克服铁芯的磁损耗,可以:
增大流过线圈的电流;
或保持相同电流,并增加绕组的匝数( N_P)。
电流(安培)与匝数的乘积称为“安匝”(ampere-turns),它决定了线圈的激磁力。
假设变压器的一次绕组和二次绕组各只有一匝。在一次绕组的单匝上施加 1 V(假设无损耗),则必须流过足够的电流并产生足够的磁通,以在二次绕组的单匝上感应出 1 V。也就是说,每匝所承受的电压相同。
当磁通呈正弦变化 \Phi = \Phi_{\max}\sin(\omega t),时,匝数为 N 的绕组的感应电动势(E)的基本关系为:
\mathrm{emf} = \text{匝数} \times \text{磁通变化率}.
其中:
f —— 磁通频率,单位为赫兹, f = \omega / (2\pi);
N —— 线圈匝数;
\Phi —— 磁通量,单位为韦伯(Wb)。
这称为变压器电动势方程(Transformer EMF Equation)。对一次绕组的电动势, N 为一次绕组匝数 N_P;对二次绕组的电动势, N 为二次绕组匝数 N_S。
另请注意,由于变压器需要交变磁通才能正常工作,故不能用于变换或提供直流电压或电流,因为必须有变化的磁场才能在二次绕组中感应出电压。换言之,变压器不适用于稳态直流电压,只能用于交流或脉动电压。
若将变压器的一次绕组接至直流电源,因直流无频率,绕组感抗为零,故等效阻抗仅为铜线电阻,绕组将从直流电源吸取极大电流,引起过热直至烧毁,因 I = V/R。
变压器基础 示例 3
一个单相变压器的一次绕组有 480 匝,二次绕组有 90 匝。当在一次绕组上施加 2200 V、50 Hz 时,磁通密度的最大值为 1.1 T。计算: a) 铁芯中的最大磁通。 b) 铁芯的横截面积。 c) 二次侧感应电动势。
根据变压器电动势方程:
磁通密度与截面面积关系为
二次侧感应电动势(有效值)为
由于二次侧额定电压等于二次侧感应电动势,亦可由匝比简便计算:
变压器中的电功率
Power in a Transformer
另一项变压器基础参数是其功率等级。变压器的功率等级即电压乘以电流所得,以伏安(VA)为单位。小型单相变压器常用 VA 标称;大型电力变压器则用千伏安(kVA,1 kVA = 10³ VA)或兆伏安(MVA,1 MVA = 10⁶ VA)标称。
在理想变压器中(忽略所有损耗),二次侧可提供的视在功率等于一次侧吸收的视在功率。变压器仅改变电压与电流的比值,不改变功率。因此,其功率比为一(unity):
也就是说,一次侧在某一电压/电流水平上的电功率会“变换”到相同频率、功率不变的二次侧。虽然变压器可升压(step-up)或降压(step-down),但无法升高功率;升压时电流相应下降,降压时电流相应上升,以保证
变压器功率
其中: \Phi_P 是一次侧相位角, \Phi_S 是二次侧相位角。
注意,功率损耗与传输电流的平方成正比,即 I^2R。将电压提高一倍( \times2)时,在提供相同功率的前提下,电流会减半( \div2),因而损耗减少到原来的 1/4。若将电压提高 10 倍,电流同样减少 10 倍,整体损耗则减少到原来的 1/100。
因为损耗与电流平方成正比( I^2R),提高输电电压(如乘以 2)会使电流减半,从而使铜损减少到原来的四分之一;电压若提高 10 倍,电流减至十分之一,损耗则仅为原来的 1/100。
变压器基础-效率
Transformer Efficiency 变压器在传递能量时不需要任何运动部件。这意味着不存在与其他电机相关的摩擦或风扇损耗。然而,变压器确实存在两种主要损耗,称为铜损和“铁损,但通常这些损耗都很小。
铜损Copper losses,也称为 I^2R 损耗,是由于电流在变压器铜绕组中循环所产生的热量损失,因而得名。铜损是变压器运行中最大的损耗。每个绕组的实际损耗功率可通过将电流平方后乘以绕组电阻来计算( I^2R)。
铁损Iron losses,也称为磁滞损耗,是铁芯中的磁分子在交变磁通作用下发生翻转时的滞后现象。由于磁分子的翻转需要能量,它们在磁通足够强才能逆转;翻转过程中产生摩擦,使铁芯发热,形成功率损耗。通过采用特殊钢合金层压铁芯,可减少磁滞损耗。
功率损耗的大小决定了变压器的效率。变压器效率反映为一次侧(输入)与二次侧(输出)绕组之间的功率损失。变压器的效率 \eta 等于二次绕组输出功率 P_S 与一次绕组输入功率 P_P 之比,因而通常很高。
理想变压器的效率为 100%,能将一次侧接收到的所有电能全部传递至二次侧。但实际变压器并非 100% 高效,在满载运行时其最高效率约为 94%–96%,对于电气设备而言已相当优秀;在恒定交流电压和频率下运行时,效率可高达 98%。
变压器的效率 \eta 表示为:
Transformer Efficiency
其中:输入、输出和损耗均以功率单位表示。
在变压器中,为了区别一次侧与二次侧的功率,一次侧的瓦特常称为“伏安”(VA)。则上述效率公式可改写为:
在学习变压器基础知识时,有时使用图示来记忆变压器的输入、输出和效率之间的关系更为简便。这里将 VA、W 和 η 三个量叠加到一个三角形中,瓦特(功率)置于三角形顶部,伏安(VA)和效率位于底部两个角。该布局对应了各量在效率公式中的实际位置。如图所示:
Transformer Efficiency Triangle
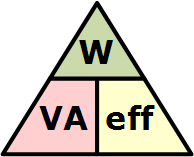
从三角图中,可以得到以下等价关系:
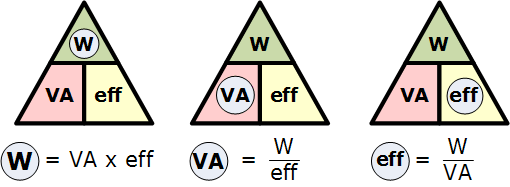
然后,计算瓦特(输出) = VA × 效率;或计算伏安(输入) = 瓦特 / 效率;或计算效率 = 瓦特 / VA;等等。
变压器基础知识总结
Transformer Basics Summary
总结本变压器基础教程:变压器利用磁场将其输入绕组上的电压(或电流)水平转换为输出绕组上的另一数值。变压器由两个电气隔离的线圈组成,工作原理基于法拉第的“互感”原理,即一次绕组中流动的电压和电流产生的磁通,在二次绕组中感应出电动势。
一次绕组和二次绕组都绕制在由单片叠装而成的软铁芯上,以减少涡流和功率损耗。变压器一次绕组连接到必须呈正弦波的交流电源,而二次绕组则向负载提供电能。需要注意的是,只要满足电压和电流的额定要求,变压器也可反向使用,将电源接在二次绕组上。
我们可以用下面的框图来表示这一变压器基础原理:
变压器基本示意图

变压器一次绕组与二次绕组匝数之比决定了它是升压变压器还是降压变压器,该比值(一次侧匝数与二次侧匝数之比)称为“匝比”或“变比”。
如果该比值小于 1(n<1),则二次侧匝数大于一次侧匝数,变压器被称为升压变压器;如果该比值大于 1(n>1),即一次侧匝数大于二次侧匝数,则变压器被称为降压变压器。
如果等于1,则为阻抗变压器
注意,只要变压器在其额定伏安(VA)范围内工作,单相降压变压器也可以通过互换接线方式,将低压绕组作为一次侧使用,从而作为升压变压器使用,反之亦然。
如果匝比等于 1(n=1),那么一次侧和二次侧的匝数相同,因而一次侧和二次侧的电压、电流也相同。
这种 1︰1 的变压器称为隔离变压器,因为其一次侧和二次侧的每匝电压相同。变压器的效率定义为其向负载输出的功率与从电源吸收的功率之比。在理想变压器中无任何损耗,因此有 P_{\text{IN}}=P_{\text{OUT}}。
在下一节关于变压器基础的教程中,我们将研究变压器的物理结构,并了解用于支撑一次侧和二次侧绕组的不同磁性铁芯类型和层叠工艺。
附录
电磁互换的本质
电和磁能相互“转换/互换”,归根结底是因为它们其实只是同一种电磁场(electromagnetic field)的两个表现分量。在经典电磁学和狭义相对论框架下,这种“互换”可以从以下几个方面理解:
1. 法拉第电磁感应(时变磁生电场)
法拉第–麦克斯韦方程之一:
说明磁感应强度 \mathbf{B}随时间变化时,在周围空间必然“激发”一个旋转的电场 \mathbf{E}(即感应电场)。
2. 位移电流(时变电生磁场)
麦克斯韦–安培定律(带位移电流项):
其中
\mathbf{J} 是电流密度,
\varepsilon_0 与 \mu_0 分别是真空电容率和磁导率。
当电场 \mathbf{E} 随时间发生变化时,位移电流项
就相当于一个“虚拟电流”,会在空间中产生磁场 \mathbf{B}。
3. 麦克斯韦方程组的对称性
完整的真空中麦克斯韦方程组(无自由电流 \mathbf{J}=0、无自由电荷 \rho=0):
可以看到,“时变电场→磁场”“时变磁场→电场”是完全对称的。
4. 狭义相对论视角:电磁场张量
在狭义相对论中,电场与磁场是统一的电磁场张量 F^{\mu\nu} 的不同分量:
在不同惯性系之间做洛伦兹变换时, F^{\mu\nu} 的分量会“混合”——有的原来看作纯电场的分量,变换后会部分表现为磁场,反之亦然。这表明电和磁并非两种独立场,而是统一电磁场在不同参考系下的投影。
5. 物理直观
变化才会产生:静止的、恒定的 \mathbf{E} 或 \mathbf{B} 不会互相转换,只有时变才会互感。
能量传递:电磁波(例如光)本身就是电、磁场相互转换并传播能量的过程。
工程应用:变压器中一次侧的交变电流先在铁芯中激发变化磁通,再在二次侧感应出电压;天线辐射/接收也是电场与磁场相互耦合的体现。
电磁“互换”并非偶然现象,而是由麦克斯韦方程组和相对论电磁场本质决定的——时变的电场必生磁场,时变的磁场必生电场;在不同参考系下,二者又可相互转换。
为什么变压器的匝比必然等于电压比
下面从更完整的电磁理论和等效模型出发,详细阐述为何理想变压器的匝比必然等于电压比。
1. Maxwell–Faraday 电磁感应定律
在微分形式下,法拉第定律给出任意闭合回路上感应电动势与穿过该回路的磁通变化率的关系:
两边对某绕组面积 S 做积分,并利用斯托克斯定理,可得:
其中
\mathbf{E} 是电场强度,
\mathbf{B} 是磁感应强度,
\Phi = \displaystyle\int_S \mathbf{B}\cdot\mathrm{d}\mathbf{S} 为穿过该绕组的磁通,
e 为该绕组上感应电动势(电压的瞬时值)。
对第 N 匝的绕组,总电压为各匝电动势之和:
2. 理想变压器的基本假设
为了简化分析,我们做出以下理想化假设:
完全耦合:一次、二次绕组产生的磁通全都耦合于同一铁芯,无漏磁;
无损耗:绕组电阻为零,无绕组电阻压降;铁芯无涡流和磁滞损耗;
线性磁化:铁芯工作点未饱和,磁化曲线在工作区近似线性。
在此条件下,一次侧与二次侧的磁通\Phi(t) 完全相同,并由同一励磁电流决定。
3. 时间域推导
分别对一次、二次绕组应用法拉第定律:
这里注意正负号约定:一次侧端点对绕组方向感应电压为负,二次侧取相同方向则为正。若统一取幅值,则可写
将二者相除,得到
其中 V_P、 V_S 是一次、二次侧的有效值电压。
4. 频域(相量)视角
在稳态正弦激励下,磁通可写成相量 \Phi(t)=\Re\{\Phi \,e^{j\omega t}\},则
相量形式下:
因此相量比也成立:
5. 能量与功率一致性
理想变压器中无损耗,输入功率等于输出功率:
又由磁通相同、线性关系可证明 \varphi_P=\varphi_S 且
这样电压比与电流比又恰好互为倒数,保证功率守恒:
6. 物理直观
匝数越多:每次磁通变化穿过更多线圈,感应电压越大;
匝比决定分压:绕组等同于无源感应元件,电压按匝数自动分布,无需任何“额外”机制;
线性性质:只要磁路和材料不饱和,比例关系恒定不变。
下面给出法拉第–麦克斯韦电磁感应定律(Maxwell–Faraday 方程)从积分形式到微分形式的经典推导过程。
Maxwell–Faraday 方程推导
1. 法拉第电磁感应实验 → 积分形式
法拉第的实验表明,当磁通量 \Phi_B随时间变化时,闭合导体回路中会产生感应电动势,其大小等于磁通量变化率的负值:
这里
是穿过任意开口面 S(t) 的磁通。若取定方向(右手法则),则在对应回路( \partial S)上测得的感应电动势可以用环路积分表述为:
因此,法拉第–麦克斯韦积分形式为:
2. 应用斯托克斯定理 → 微分形式
根据斯托克斯(Stokes)定理,任意光滑曲面 S 及其边界曲线 \partial S 满足:
将此代入积分形式,即得
如果此等式对任意曲面 S 都成立,则积分内的场量必一一对应,从而可写成点形式(微分形式):
斯托克斯定理(Stokes’ Theorem)
设 S 是三维空间中一块光滑有向曲面, \partial S 是其有向边界闭合曲线; \mathbf{F}(\mathbf{r}) 是定义在 S 上的光滑向量场,则有:
\boxed{ \oint_{\partial S} \mathbf{F}\cdot\mathrm{d}\boldsymbol{\ell} = \iint_{S} \bigl(\nabla \times \mathbf{F}\bigr)\cdot\mathrm{d}\mathbf{S} }.
其中:
\displaystyle\oint_{\partial S}\mathbf{F}\cdot\mathrm{d}\boldsymbol{\ell} 是沿着边界曲线 \partial S 的线积分,方向由右手定则(曲面法向给定时,曲线方向按右手螺旋规则确定);
\displaystyle\nabla\times\mathbf{F} 是向量场的旋度(Curl);
\displaystyle\iint_{S}(\nabla\times\mathbf{F})\cdot\mathrm{d}\mathbf{S} 是在曲面 S 上对旋度的曲面积分, \mathrm{d}\mathbf{S} 的方向与 \partial S 上的积分方向匹配。
数学条件
曲面 S 和边界 \partial S 必须可分片光滑(Piecewise Smooth)且有向;
向量场 \mathbf{F} 在包含 S 的区域内连续且具有连续的偏导数。
斯托克斯定理是向量分析中的桥梁,将“局部的旋转性质”(旋度)与“整体的环流效果”(线积分)统一起来,是电磁学、流体力学等诸多领域的基石。
3. 小结
积分形式
\displaystyle \oint_{\partial S} \mathbf{E}\cdot\mathrm{d}\boldsymbol{\ell} = -\,\dfrac{\mathrm{d}}{\mathrm{d}t}\displaystyle\int_{S}\mathbf{B}\cdot\mathrm{d}\mathbf{S}.微分形式
\displaystyle \nabla\times\mathbf{E} = -\,\frac{\partial\mathbf{B}}{\partial t}.
它们之间的等价性,正是通过斯托克斯定理将环路积分与曲面积分联系起来所实现的。这样,法拉第–麦克斯韦电磁感应定律就从实验经验(磁通变化产生电动势),严格推导到场论的微分方程形式。
铁损详情
铁损(Iron Loss) 铁损是指变压器铁芯在交变磁通作用下产生的功率损耗,主要包括两部分:
磁滞损耗(Hysteresis Loss)
涡流损耗(Eddy‐Current Loss)
1. 磁滞损耗
机制 铁芯由大量磁畴(magnetic domains)构成。当交变磁场使磁通密度 B 在正负方向间循环时,每个磁畴的磁化方向都会滞后于外加磁场强度 H 的变化。在 B–H 坐标系下,铁芯完整的磁化过程会形成一个磁滞回线(hysteresis loop),其回线所围面积即表示每个循环中铁芯吸收并以热形式损失的能量。
定量表达 根据史坦梅茨(Steinmetz)经验公式,磁滞损耗功率可近似表示为:
P_{\rm hyst} = k_h\,f\,B_{\max}^n\quad (\mathrm{W/kg})其中
P_{\rm hyst} —— 单位质量磁滞损耗功率,单位 W/kg;
k_h —— 与材料特性相关的常数;
f —— 频率,单位 Hz;
B_{\max} —— 磁通密度最大值,单位 T;
n —— 材料指数,一般取 1.5\sim2.5。
特点
与频率成正比,与最大磁通密度的非线性高次幂成正比;
磁滞回线越“宽”,损耗越大;晶粒取向硅钢可显著缩小回线面积。
2. 涡流损耗
机制 交变磁通穿过铁芯导电回路时,根据法拉第定律在铁芯内部感应出涡流。涡流在铁芯内部流动遇到电阻产生焦耳热,形成功率损耗。
定量表达 将铁芯层压为厚度 t 的薄片、并涂绝缘层后,可近似得到:
P_{\rm eddy} = k_e\,f^2\,B_{\max}^2\,t^2\quad (\mathrm{W/kg})其中
P_{\rm eddy} —— 单位质量涡流损耗功率,单位 W/kg;
k_e —— 与材料电阻率及几何形状相关的常数;
t —— 铁芯单片厚度,单位 m;
其它符号同上。
特点
与频率的平方和最大磁通密度的平方成正比;
片厚 t 越小,涡流路径越受限,损耗越低;
3. 综合与控制
总铁损
P_{\rm iron}=P_{\rm hyst}+P_{\rm eddy}.控制方法
磁滞损耗:选用定向取向硅钢片,优化晶粒取向、降低矫顽力;
涡流损耗:采用薄片层压结构,减少单片厚度并涂绝缘层;
工作点控制:限制最大磁通密度 B_{\max} 在合理范围内,避免铁芯饱和并减小损耗。
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

