Logo

Menu

张彤
张彤
Published on 2025-07-14 / 15 Visits
1
0

3.相位差和相移

相位差和相移

Phase Difference and Phase Shift

相位差用于描述两个或多个交变量alternating quantities在达到最大值或过零点时，以度或弧度为单位的相位差异。

相量Phasors是在电路频率相同的交流电路中，用来分析各元件行为的一种有效工具。两个相量相加的结果取决于它们的相对相位relative phase，也就是因相位差而“同相”或“反相”之间的关系。

正弦波是一种可在时域沿水平轴以图形方式表示的交变量。作为时变量，正弦波在 t = \tfrac{\pi}{2} 时达到正最大值，在 t = \tfrac{3\pi}{2} 时达到负最大值，而在 t = 0、\pi 和 2\pi 处沿基线出现零值。

然而，并非所有正弦波都会在相同的时刻恰好通过零轴。当与另一条正弦波比较时，它们可能相对于 0^\circ 点向右或向左“偏移”一定角度。

例如，将电压波形与电流波形进行比较时，就会在两条正弦波之间产生角度偏移，也就是相位差。任何在 t = 0 时未通过零点的正弦波，都具有相移phase shift。

正弦波形的差异（或称相移）是指该波形相对于水平零轴上某一参考点所偏移的角度 \Phi（希腊字母 Phi），可用度或弧度表示。换言之，相移就是两个或多个波形在同一坐标轴上沿水平方向的横向差异，同频率的正弦波形之间可以存在这样的相位差。

交流波形的相位差 \Phi 在一个完整周期 T 内可取任意值，其范围为 \Phi = 0 到 \Phi = 2 \pi（弧度）或 \Phi = 0\degree 到 \Phi = 360 \degree（角度），具体取决于所使用的角度单位。

相位差也可以用时间偏移 \tau（以秒为单位）来表示，表示为周期 T 的一部分，例如 +10 ms 或 –50 μs，但通常更常用角度来度量相位差。

Tau 是圆的周长与半径的比值，约等于 2\pi，用于计算圆的弧度数

因此，我们在前一节“正弦波形”中推导出的正弦电压或电流波形的瞬时值方程，需要加入相位角的修正，新的一般表达式变为：

相位差方程

Phase Difference Equation

A_{(t)} = A_{max} \times \sin(\omega t + \Phi)


其中：

  • A_m —— 波形的幅值（振幅）。

  • \omega t —— 波形的角频率，单位为弧度/秒。

  • \Phi（Phi）—— 波形相对于参考点左右偏移的相位角，单位为度或弧度。

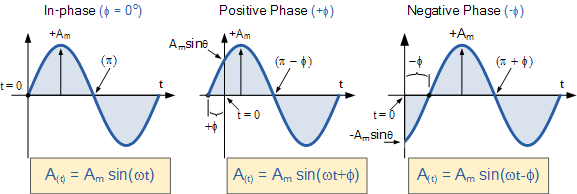
如果正弦波的正斜率在 t = 0 之前穿过水平轴，则波形相对于参考点向左移动，此时 \Phi > 0，相位角为正（ + \Phi），产生超前相位角。换句话说，它在时间上早于 0° 出现，使得相量逆时针方向旋转。

同样地，如果正弦波的正斜率在 t = 0 之后才穿过水平轴，则波形向右移动，此时 \Phi < 0，相位角为负（ –\Phi），产生滞后相位角，因为它在时间上晚于 0° 出现，使得相量顺时针方向旋转。下图展示了这两种情况。

正弦波的相位关系

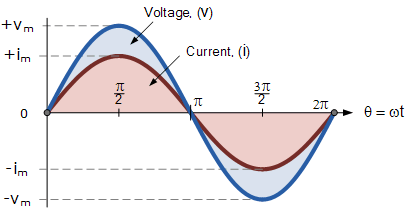
首先，假设两个交流量——电压 v和电流 i——具有相同的频率 f（赫兹）。由于它们的频率相同，其角速度 \omega 也必然相同。因此，在任一时刻，我们可以说电压 v 的相位与电流 i 的相位是相同的。

这样，在一个给定时间段内的旋转角度始终一致，电压 v 与电流 i 之间的相位差 \Phi 为零。因为 v 和 i 的频率相同，它们在一个完整周期内会同时达到正峰值、负峰值和过零点（尽管它们的幅值可能不同）。此时，这两个交流量 v 和 i 被称为“同相”（in-phase）。

两个同相正弦波

现在假设电压 v 和电流 i 之间存在 30^\circ 的相位差，即 \Phi = 30^\circ 或 \pi/6 弧度。由于这两种交流量以相同的角速度（即相同频率）旋转，这一相位差在任何时刻都保持不变。下图即用 \Phi 表示两者之间的 30^\circ 相位差。

正弦波的相位差

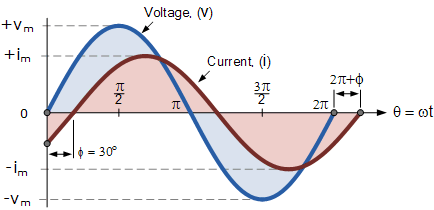
上图中的电压波形在 t=0 时刻从水平参考轴的零点开始，而在同一时刻，电流波形的值仍为负，直到晚于 30° 时才穿过参考轴。也就是说，电流波形在电压波形之后才达到过零点和最大值／最小值，从而两者之间产生了相位差。

由于这两条波形不再“同相”in phase，它们之间存在由 \Phi 决定的“异相”out-of phase量，在本例中为 30°。因此可以说，这两条波形相差 30°。电流波形相对于电压波形“滞后”了相位角 \Phi(Lagging Phase Difference)。在上述例子中，由于相位差为滞后型，电压和电流的瞬时表达式可写为：

电压波形：

\text{Voltage, }(v_t) = V_m \sin \omega t

电流波形：

\text{Current, }(i_t) = I_m \sin\bigl(\omega t - \phi\bigr)

其中：

  • V_m、I_m 分别为电压和电流的最大幅值；

  • \omega 为角频率（弧度/秒）；

  • \Phi 为相位差。

同样地，如果电流 i 的正值在电压 v 之前穿过水平参考轴，并先于电压达到过零点和最大峰值，那么电流波形相对于电压波形“超前”了一定的相位角(Leading Phase Difference)。此时两条波形被称为具有“超前相位差”（Leading Phase Difference），对应的电压和电流瞬时表达式为：

\text{Voltage, }(v_t) = V_m \sin \omega t
\text{Current, }(i_t) = I_m \sin\bigl(\omega t + \phi\bigr)

  • 电流 i 相对于电压 v “超前”相角 \phi

正弦波的相位角可用来描述同频率正弦波之间的关系，通过“超前”（Leading）和“滞后”（Lagging）这两个术语来表示它们在同一参考轴上的相互位置。在上面的例子中，两条波形相位差为 30°。因此，我们既可以说 i 相对于 v 滞后 30°，也可以说 v 相对于 i 超前 30°，具体取决于选择哪个作为参考。

两条波形之间的关系及其相位角，可在任意位置沿水平零轴上测量，只要两者在该点具有相同方向的斜率（正向或负向）。

在交流电力电路中，能够描述同一回路中电压和电流正弦波关系的能力十分重要，并且构成了交流电路分析的基础。

余弦波形

The Cosine Waveform

现在我们知道，如果一个波形相对于另一条正弦波向右或向左“偏移”了 0^\circ，那么该波形的表达式变为

A_m\sin(\omega t \pm \Phi)\,


但是，如果一个波形在参考波形之前，以正斜率提前 90^\circ（或 \pi/2 弧度）穿过水平零轴，那么该波形就称为“余弦波”，其表达式变为：

余弦表达式

\sin(\omega t + 90^\circ) = \sin\!\Bigl(\omega t + \frac{\pi}{2}\Bigr) = \cos(\omega t)

余弦波，简称 “cos”，在电气工程中与正弦波同样重要。余弦波与正弦波具有相同的波形——它们都是正弦函数——但余弦波相对于正弦波提前了 +90°（相当于一个周期的四分之一）。

正弦波与余弦波的区别

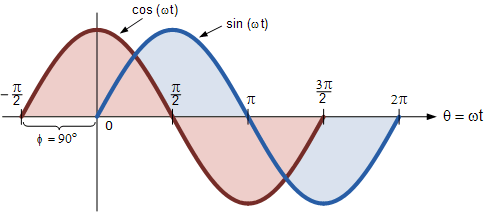
或者，我们也可以说，正弦波是相对于余弦波向相反方向偏移了 −90° 的波形。无论以哪种方式，在处理带有相角的正弦波或余弦波时，以下规律始终适用。

正弦波和余弦波的关系

\cos(\omega t + \phi) = \sin\bigl(\omega t + \phi + 90^\circ\bigr)
\sin(\omega t + \phi) = \cos\bigl(\omega t + \phi - 90^\circ\bigr)

在比较两个正弦波形时，通常更常用将它们的关系表示为具有正向振幅的正弦或余弦形式，这可以通过以下数学恒等式来实现。

\sin(A \pm B) = \sin(A)\cos(B) \pm \cos(A)\sin(B)
\cos(A \pm B) = \cos(A)\cos(B) \mp \sin(A)\sin(B)
-\sin(\omega t) = \sin\bigl(\omega t \pm 180^\circ\bigr)
-\cos(\omega t) = \cos\bigl(\omega t \pm 180^\circ\bigr)
\pm \sin(\omega t) = \cos\bigl(\omega t \mp 90^\circ\bigr)
\pm \cos(\omega t) = \sin\bigl(\omega t \pm 90^\circ\bigr)

通过利用上述这些恒等关系，我们可以将任何带有或不带有角度／相位差的正弦波，在正弦形式和余弦形式之间相互转换。

在下一节关于相量（Phasors）的教程中，我们将采用图解法来表示或比较两条正弦波之间的相位差：首先观察单相交流量的相量表示，然后结合相量代数，来进行两个或多个相量的数学相加。

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。

2.正弦波形
4.相量图与相量代数

Comment