电容与电荷

Capacitance and Charge

电容器以电荷的形式在其极板上储存电能。

电容（capacitance）是衡量电容器储存电荷能力的量值。该电容值也取决于用于分隔两块平行极板的电介质材料的介电常数。电容的单位是法拉（\mathrm{F}），以迈克尔·法拉第命名。

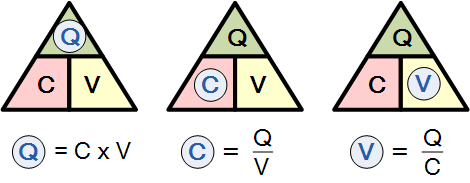
电容器由两块平行的导电极板（通常为金属）组成，它们由称为“电介质”的绝缘材料隔开，防止彼此接触。当电压施加到这些极板上时，会产生电流，使一块极板带相对于电源电压的正电荷，而另一块极板带等量相反的负电荷。

因此，电容器能够储存电荷 Q（单位库仑，\mathrm{C}）。当电容器充满电后，其极板之间会存在电势差（p.d.）。极板面积越大和／或极板间距离（称为“极板间距”）越小，电容器所能储存的电荷越多，其电容也越大。

已知电容为 C（单位 \mathrm{F}）时，电容器在极板间储存的电荷 Q 与施加电压 V 成正比：

注意，电容 C 始终为正值，绝不为负值。

施加的电压越大，电容器极板上存储的电荷越多；反之，施加的电压越小，存储的电荷越少。因此，电容器极板上的实际电荷 Q 可以通过以下公式计算：

电容器上的电荷 (Q)

其中：

有时通过图示来记忆这个关系会更容易。这里将三个量 Q、C 和 V 叠加在一个三角形中，电荷置于顶端，电容和电压置于底部。此布局对应于电容器电荷公式中各量在三角图中的实际位置。

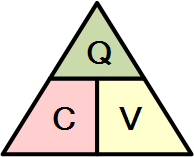
通过对上述等式进行移项，可得到同一公式的以下几种组合形式：

单位：

由此可将电容的单位定义为比例常数，即库仑/伏特，也称为法拉（ \mathrm{F}）。

由于电容表示电容器在其极板上储存电荷的能力，我们可以将一法拉定义为“在其极板之间建立 1\ \mathrm{V} 电势差时所需电荷量为 1\ \mathrm{C} 的电容”，该定义最早由迈克尔·法拉第提出。因此，在相同电压下，电容越大，电容器所储存的电荷越多。

电容器在导电极板上储存电荷的能力赋予了它电容值。电容还可以由极板的尺寸或面积 A 以及极板之间电介质材料的性质来确定。电介质材料的量度由介电常数 \varepsilon 给出。因此，另一种表达电容器电容的方法为：

带空气作为电介质的电容器

Capacitor with Air as its dielectric

带固体作为电介质的电容器

Capacitor with a Solid as its dielectric

其中，

• A 为极板面积，单位为平方米（\mathrm{m}^2），面积越大，电容器所能储存的电荷越多；

• d 为两极板之间的距离（或间隔），距离越小，极板储存电荷的能力越强，因为带 -Q 的极板对带 +Q 的极板作用力更大，从而有更多电子被排斥出带 +Q 的极板，增加整体电荷量；

• \varepsilon_0（真空介电常数）为

  \varepsilon_0 = 8.854\times10^{-12}\ \mathrm{F/m},

• \varepsilon_r 为所用电介质材料的相对介电常数。

平行板电容器

Parallel Plate Capacitor

我们之前已说明，对于平行板电容器，当电介质为空气时，其电容与极板面积 A 成正比，与极板间距离 d 成反比：

然而，通过在导电极板之间插入介电常数大于空气的固体介质，可提高电容值。

常用介电材料的介电常数 \varepsilon（相对于真空）的典型取值如下：

• 空气： \varepsilon=1.0

• 纸： \varepsilon=2.5\text{–}3.5

• 玻璃： \varepsilon=3\text{–}10

• 云母： \varepsilon=5\text{–}7

介电常数（Dielectric Constant，记作 k）定义为该介电材料相对于真空（真空介电常数 \varepsilon_0）对电容的增益倍数：

因此，所有电容值均与真空介电常数相关。介电常数越高，作为绝缘体时对电容的增强作用越显著。由于 k 为比值量，故无量纲。

电容示例 1

一个平行板电容器由两块极板组成，总表面积为 100\ \mathrm{cm}^2。如果极板间距为 0.2\ \mathrm{cm}，所用介质为空气，则该电容器的电容（以皮法拉，pF 为单位）为多少？

首先，利用平行板电容公式：

其中

因此

电容器的充放电

Charging & Discharging of a Capacitor

考虑下列电路。

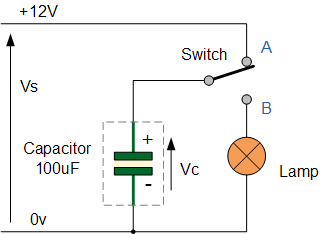
假设电容器已完全放电，并且与电容器相连的开关刚刚移至位置 A。此时， 100\,\mu\mathrm{F} 电容器两端的电压为零，将有一个充电电流 i 开始流动，电容器按指数规律充电，直到极板两端的电压几乎等于 12\,\mathrm{V} 电源电压。经过 5 个时间常数后，电流变为涓流，此时称电容器“已完全充电”。于是有

从理论上讲，一旦电容器“完全充电”后，即使断开电源电压，它也能保持其电荷状态，因为电容器在某种程度上充当了临时储能装置。然而，虽然这对于“理想”电容器成立，但对于实际电容器而言，由于内部泄漏电流流经电介质，它会在较长时间内缓慢放电。

这是一个需要注意的重要点：当大容量电容器并联在高压电源上时，即使电源电压被切断，它们仍能保持大量电荷。

如果此时将开关断开，电容器将理论上无限期保持其电荷，但由于内部泄漏电流穿过电介质，电容器会非常缓慢地开始放电。电容器放电至其电源电压的 37%（即 0.37\,V_S）所需的时间称为其时间常数Time Constant。

如果现在将开关从位置 A 移至位置 B，完全充电的电容器将通过并联的灯泡开始放电，使灯泡点亮，直到电容器完全放电为止，因为灯泡元件具有电阻值。

灯泡的亮度和点亮时间最终取决于电容器的电容值和灯泡的电阻：

电容值越大，可储存的电荷越多，灯泡就越亮且点亮时间越长。

电容示例 2

计算上述电容电路中的电荷。

因此，电容器上的电荷为 1.2\,\mathrm{mC}。

电容器中的电流

Current through a Capacitor

由于两极板之间电介质材料的绝缘特性，电流实际上不能像电阻或电感那样流过电容器。然而，两极板的充电和放电过程产生了电流流动的效应。

流过电容器的电流与极板上的电荷直接相关，因为电流是电荷相对于时间的流动速率。由于电容器在极板之间储存电荷 Q 的能力与施加电压 V 成正比，电容器两极板上所施加电压与电流之间的关系可表示为：

电流—电压（I–V）关系

Current-Voltage (I-V) Relationship

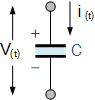
由于两极板之间电介质的绝缘特性，电流并不能像在电阻或电感中那样真正“流经”电容器。然而，两极板的充电与放电过程会产生电流流动的等效效应。

随着极板两端电压随时间的增加（或减少），流过电容器的电流会向极板存入（或移除）电荷，存入的电荷量与施加电压成正比。此时，电流与电压均为时间的函数，分别记作

从上述关系也可看出：如果电压保持恒定，则电荷量 Q 始终不变，因而电流 i=\frac{\mathrm{d}Q}{\mathrm{d}t}=0。换言之，“无电压变化，无电荷移动，无电流流动”，这正是电容器在稳态直流电压下“阻断”直流电流的原因。

电容值 — 法拉

Capacitance Value – The Farad

电容器储存电荷的能力决定了其电容值 C，单位为法拉（ \mathrm{F}）。但法拉本身是一个极大的单位，实际应用中常用其子倍单位。

假设在真空中，两极板间距 d=1\ \mathrm{mm}=0.001\ \mathrm{m}，要得到 1\ \mathrm{F} 的电容，所需极板面积可由

变形得

相当于边长超过 10\ \mathrm{km}\times10\ \mathrm{km}（超 6 英里）的正方形区域，可见一法拉之巨大。

具有 1\,\mathrm{F} 或更大值的电容器通常采用固体电介质；在电子电路中，常用以下子倍单位：

电容的子单位

Capacitance Sub-units of the Farad

微法拉（\mu\mathrm{F}）

纳法拉（\mathrm{nF}）

皮法拉（\mathrm{pF}）

将下列电容值换算： 22\,\mathrm{nF} 转换为 \mu\mathrm{F} 得

0.2\,\mu\mathrm{F} 转换为 \mathrm{nF} 得

550\,\mathrm{pF} 转换为 \mu\mathrm{F} 得

虽然一法拉本身是一个很大的单位，但目前市面上已有电容量达数百法拉的电容器，通常被称为“超级电容器（Super-capacitors）”或“超容（Ultra-capacitors）”。这些电容器是一种电化学储能装置，利用碳电极的高表面积来提供远高于传统电容器的能量密度；由于电容与碳电极的表面积成正比，碳层越厚，电容值越大。低电压（约 3.5V 至 5.5V）超级电容器因其高电容值能够储存大量电荷，其储能可表示为

低电压超级电容器常用于便携式手持设备，以替代体积大、昂贵且沉重的锂电池，因为它们具有类电池的存储和放电特性，非常适合作为备用电源或内存备份；手持设备中的超级电容器通常通过安装在设备上的太阳能电池充电。超容正被开发用于混合动力汽车和替代能源领域，以取代大型传统电池，并用于车辆音视频系统的直流平滑；由于超容可快速充电且具有极高的能量存储密度，使其成为电动汽车等应用的理想选择。

电容器中的能量

Energy in a Capacitor

当电容器从所连接的电源充电时，会在电容器内部建立一个静电场，该静电场储存能量。储存在该静电场中的能量（单位为焦耳， \mathrm{J}）等于电压电源为维持电容器极板上电荷所做的功，其表达式为：

因此，上述 100\,\mu\mathrm{F} 电容电路中储存的能量计算如下：

在本节关于电容器的下一篇教程中，我们将学习电容器色环代码（Capacitor Colour Codes），并了解电容器外壳上电容值和额定电压的各种标记方式。

附录

电容和电池的区别

各种储能材料/器件的典型能量密度和功率密度

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。