功率三角形与功率因数
Power Triangle and Power Factor
在交流电路中消耗的电功率可以用一个直角三角形的三条边来表示,这个三角形通常被称为功率三角形。
在我们关于电功率的教程中已经看到,含有电阻与电容、或电阻与电感,或同时含有这两类元件的交流电路,既存在有功功率,也存在无功功率。因此,若要计算并绘制表示总消耗功率的功率三角形,我们需要知道电压与电流正弦波形之间的相位差。
在交流电路中,电压和电流波形都是正弦波,其幅值随时间不断变化。因为电功率等于电压乘以电流 (P = V·I),所以当电压和电流两条波形完全重合,即它们的波峰和零交叉点在同一时刻出现时,功率达到最大值。这种情况被称为“同相”。
在交流电路中,会影响电压与电流波形关系(从而影响它们相位差)并决定电路总阻抗的主要元件有三种:电阻 (R)、电容 (C) 和电感 (L)。
交流电路的阻抗 ( Z) 与直流电路中计算得到的电阻等效,单位同为欧姆。在交流电路中,阻抗通常定义为电路元件产生的电压与电流相量之比。相量用直线表示,其长度代表电压或电流的幅值,而其相对于其他相量的角度位置表示相位差。
交流电路同时包含电阻和电抗,两者共同作用产生总阻抗 ( Z),从而限制电流在电路中的流动。但交流电路的阻抗并不等于纯电阻值与纯电抗值的代数和,因为纯电阻与纯电抗之间存在 90° 的相位差。
不过,我们可以把这 90° 的相位差视为直角三角形的两条直角边,称为阻抗三角形,其中阻抗是由毕达哥拉斯定理确定的斜边。
电阻、电抗与阻抗之间的几何关系可以通过阻抗三角形直观地表示,如下图所示。
阻抗三角形
Impedance Triangle
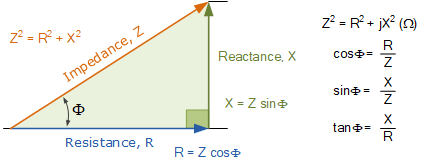
请注意,阻抗是电阻与电抗的向量和,因此不仅具有大小 \,Z\,,还具有相位角 \,\Phi\,,该角度表示电阻与电抗之间的相位差。又因为电抗 \,X\, 会随频率变化而改变,所以随着频率变化,三角形的形状也会随之改变;而电阻 \,R\, 始终保持不变。
我们可以更进一步,将阻抗三角形转换为功率三角形,以表示交流电路中的三种功率分量。欧姆定律告诉我们,在直流电路中功率 \,P(单位瓦特)等于电流平方 \,I^{2}\, 乘以电阻 \,R。因此,只需把阻抗三角形的三条边都乘以 \,I^{2}\,,即可得到对应的功率三角形:
有功功率: \displaystyle P = I^{2}R\quad\text{(W)}
无功功率: \displaystyle Q = I^{2}X\quad\text{(VAr)}
视在功率: \displaystyle S = I^{2}Z\quad\text{(VA)}
交流电路中的有功功率
Real Power in AC Circuits
有功功率 \,P\,(也称真功或活性功率)在电路中完成“实际做功”。它以瓦特计量,定义了电路中电阻部分所消耗的功率。因此在交流电路中,有功功率仍按 \,P = I^{2}R\, 计算,其中 \,R\, 为电路的总电阻分量。
由于纯电阻不会在电压与电流波形之间产生任何相位差(相移),所有有用功率都直接加在电阻上,转换为热能、光能或机械功。因此电阻消耗的功率就是有功功率,本质上等于电路的平均功率。
要计算有功功率,只需将电压和电流的 rms 值与相位角 \Phi 的余弦相乘,具体如下所示:
由于在纯电阻电路中电压与电流之间不存在相位差,两条波形的相移为零 (0)。因此:
其中,有功功率 P 以瓦特 (Watt) 为单位,电压 V 采用 rms 值(伏特),电流 I 亦采用 rms 值(安培)。
因此,有功功率就是由电阻分量消耗的 \,I^{2}R 功率,计量单位为瓦特 (W),也是电能表上读到的数值,常用单位包括瓦特 (W)、千瓦 (kW) 和兆瓦 (MW)。注意,有功功率 P 始终为正值。
交流电路中的无功功率
Reactive Power in an AC Circuit
无功功率 Q(亦称 wattless power)是在交流电路中消耗但不做任何有用功的功率,却对电压与电流波形之间的相位差产生显著影响。无功功率与电感和电容产生的电抗相关,并抵消有功功率的效果;在直流电路中则不存在无功功率。

不同于承担全部做功能力的有功功率 P,无功功率 Q 因电感磁场与电容静电场的建立与释放而从电路中“吸走”功率,使真正的有功功率更难直接向负载供能。
电感在磁场中储存的能量倾向于控制电流;
电容在静电场中储存的能量倾向于控制电压。
结果是:电容“发出”无功功率,而电感“吸收”无功功率。两者既吸收又向电源返回能量,因此并不消耗任何有功功率。
计算无功功率时,将电压和电流的 rms 值乘以相位角 \Phi 的正弦:
在纯电抗(纯电感或纯电容)电路中,电压与电流波形相差 90^{\circ}。因此,用 \,V I \sin\Phi 得到的分量与电压、电流彼此相差 90^{\circ},这就是交流电路中的无功功率。
在这里,无功功率 Q 的单位是伏安·无功(VAr),电压 V 采用 \mathrm{rms} 值(伏特),电流 I 也采用 \mathrm{rms} 值(安培)。
因此,无功功率表示相位相差 90^{\circ} 的电压与电流所产生的伏安乘积;一般情况下,电压与电流之间可以存在任意相位角 \Phi。
于是,无功功率就是电路中 \,I^{2}X 的电抗分量,其单位包括伏安·无功(VAr)、千伏安·无功(kVAr)和兆伏安·无功(MVAr)。
“Q”来源于拉丁/德文 “Quadratur”,意思是与电压或电流相位相差 90°(即“正交”)的那部分功率。
无功功率不做实际功(不消耗电能),而是在电源和电感、电容等储能元件间来回交换:
电感:吸收能量后滞后返回,Q > 0(感性负载)
电容:吸收能量后超前返回,Q < 0(容性负载)
交流电路中的视在功率
Apparent Power in AC Circuits
前面我们已看到,有功功率由电阻耗散,而无功功率由电抗(电感或电容)提供。由于电路的电阻分量和电抗分量不同,电压与电流波形不会同相。
因此,有功功率 P 与无功功率 Q 之间存在一个数学关系,称为复功率。将交流电路所加 \mathrm{rms} 电压 V 与流过的 \mathrm{rms} 电流 I 相乘,得到的“伏安乘积”称为 视在功率,符号为 S(单位 VA)。
复功率并非简单的 P 与 Q 的代数和,而是两者的向量和;用功率三角形即可表示这种几何关系。伏安乘积的 \mathrm{rms} 值通常就称为视在功率,因为“表面上”这似乎是电路消耗的总功率,尽管真正做功的有功功率要小得多。
视在功率包含两部分:
电阻功率——同相功率,即有功功率(瓦特);
电抗功率——相差 90^{\circ} 的功率,即无功功率(伏安·无功)。
将这两部分功率作向量相加,可用功率三角形表示。功率三角形由四个要素组成: P、Q、S 和 \theta。
与前面讨论的阻抗三角形类似,交流电路中的三种功率成分也可用直角三角形的三条边来图示:
水平(邻边)为电路的有功功率 P;
垂直(对边)为电路的无功功率 Q;
斜边为结果视在功率 S。
这就是交流电路的功率三角形。
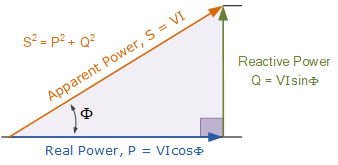
其中:
P 是 \displaystyle I^{2}R——有功功率,执行实际做功,单位瓦特(W)
Q 是 \displaystyle I^{2}X——无功功率,单位伏安·无功(VAr)
S 是 \displaystyle I^{2}Z——视在功率,单位伏安( VA)
\Phi 为相位角(°); \Phi 越大,无功功率越大
\cos\Phi \;=\; \frac{P}{S}\;=\;\frac{\text{W}}{\text{VA}} \quad\Bigl(\text{功率因数,p.f.}\Bigr)
\sin\Phi \;=\; \frac{Q}{S}\;=\;\frac{\text{VAr}}{\text{VA}}
\tan\Phi \;=\; \frac{Q}{P}\;=\;\frac{\text{VAr}}{\text{W}}
功率因数等于有功功率与视在功率的比值,因此 \text{p.f.} = \cos\Phi。
交流电路中的功率因数
Power Factor in AC Circuits
功率因数 \cos\Phi 是交流电路中的关键参数,也可用电路阻抗或功率来表示。它定义为有功功率 P 与视在功率 S 的比值,通常写成小数(如 0.95)或百分比(如 95 %)。
功率因数决定了电流与电压波形之间的相位角 \Phi。这里 I 和 V 均表示电流与电压的 \mathrm{rms} 幅值。无论把相位角视为“电流相对电压”还是“电压相对电流”,其数学关系均为
我们之前提到,在纯电阻电路中,电流与电压波形同相,因此由于相位差为 0^{\circ},消耗的有功功率与视在功率相同。于是功率因数为
也就是说,消耗的瓦特数与伏安数相等,产生的功率因数为 1.0(即 100 %),称为功率因数为 1(单位功率因数,unity power factor)。
我们同样提到,在纯电抗电路中,电流与电压波形之间相差 90^{\circ}。由于相位差为 90^{\circ},功率因数为
也就是说,虽然回路中仍存在电压与电流来为无功负载供能,但消耗的瓦特数为零。显然,若能减小功率三角形中的无功功率 Q( VAr 分量),则角 \theta 会减小,功率因数便会朝 1(单位功率因数)改善。较高的功率因数意味着电路向负载输送电流的效率更高。
由此,可写出有功功率 P、视在功率 S 与电路功率因数的关系式:
在感性电路中,电流“滞后”于电压(ELI),因此称该电路具有滞后功率因数;而在容性电路中,电流“超前”于电压(ICE),因此称该电路具有超前功率因数。
总结练习1
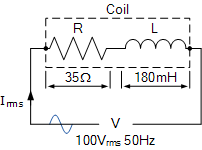
功率三角形示例 1
一只绕线线圈具有电感 180\,\text{mH} 和电阻 35\,\Omega,接在 100\,\text{V}、50\,\text{Hz} 的电源上。
计算: a) 线圈的阻抗; b) 电流; c) 功率因数; d) 视在功率。同时为上述线圈绘制功率三角形。
已知数据:
已知参数
(a) 线圈阻抗 \;Z
(b) 电流 \;I
(c) 功率因数 (pf) 与相位角 \varphi
(d) 各种功率
校核:
S = \sqrt{P^{2}+Q^{2}} \approx \sqrt{79^{2}+127.5^{2}} \approx 150\;\text{VA}\;\checkmark
(e) 功率三角形
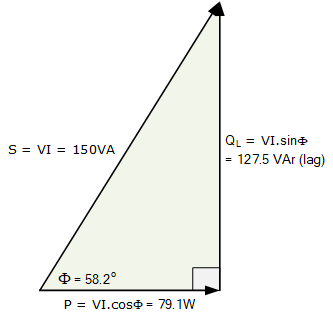
如本例中的功率三角形所示,当功率因数仅为 \,0.5263\;(52.63\%) 时,线圈必须消耗 \,150\,\text{VA} 的视在功率才能获得 \,79\,\text{W} 的有功功率。换句话说,在 \,52.63\% 的功率因数下,线圈为了完成相同的有功输出,需要额外约 \,89\% 的电流,这意味着大量电流被白白浪费。
在该线圈两端并联一个功率因数校正电容(本例中为 \,32.3\,\mu\text{F}),可将功率因数提高到 \,0.95\;(95\%) 以上,大幅降低线圈所消耗的无功功率。因为电容相当于无功电流的“发生器”,能够抵消部分感性无功电流,从而显著减少电路的总电流消耗。
功率三角形与功率因数总结
我们已经看到,交流电路中的三种电功率——有功功率、无功功率和视在功率——可以用一个称为功率三角形的三角形来表示,其三条边分别对应这三种功率。由于这是一个直角三角形,它们之间满足
其中P 为有功功率,单位瓦特 (\text{W}); Q 为无功功率,单位乏 (\text{VAr}); S 为视在功率,单位伏安 (\text{VA})。
我们还知道,在交流电路中, \cos\!\bigl(\Phi\bigr) 被称为功率因数。功率因数定义为电路消耗的有功功率与视在功率之比,因此
于是,电流与电压之间夹角 \Phi 的余弦值就是功率因数。功率因数通常以百分数(例如 95%)或小数(例如 0.95)表示。
当功率因数为 1.0(单位功率因数,100%)时, \displaystyle P=S,即有功功率等于视在功率,电流与电压的相位差为
\cos^{-1}\!\bigl(1.0\bigr)=0^{\circ}.当功率因数为 0 时,相位差为
\cos^{-1}\!\bigl(0\bigr)=90^{\circ},此时无论电路电流多大,电路实际消耗的有功功率都为零。
实际交流电路中的功率因数通常介于 0 与 1.0 之间,取决于负载内部的无源元件:
感抗-电阻负载(最常见) → 功率因数“滞后”;
容抗-电阻负载 → 功率因数“超前”。
因此,一个交流电路或负载的功率因数可以是单位、滞后或超前。
功率因数低(接近 0)会造成功率浪费,降低电路效率;而功率因数高(接近 1.0 或 100%)则代表电路效率高。这是因为功率因数低的电路/负载,要获得同样的有功输出,需要比功率因数高的电路/负载吸取更多的电流。
附录
35 kV 变电站典型无功补偿系统解析
下面以 35 kV 区域变电站为背景,从一次设备配置 → 容量计算 → 投切与控制 → 保护与谐波抑制四个层面,梳理一套常见的无功补偿系统设计思路,并给出定量示例。
1 系统运行场景与设计目标
目标:全年大部分时段将母线功率因数维持在 0.95 以上,并兼顾轻载时期电压抑制与谐波治理。
2 容量与型号选择
2.1 所需补偿无功
需在 35 kV 侧注入约 12 Mvar 容性无功。
2.2 设备组合
结构特点
“F + S”——固定电容 + 分级电容 提供经济的基波容性无功
“SVG” 提供毫秒级动态补偿与谐波滤除(部分 5、7 次)
“消弧电抗器” 或 “分段小电抗” 抑制深夜轻载电压升高
3 投切与控制逻辑
3.1 功率因数/电压双闭环
PF/|U| 控制器
┌─────────────────────────────────┐
│ 采样:I_CT, V_PT │
│ 计算:cosφ, |U| │
│ 逻辑:
│ - cosφ < 0.92 → 投电容
│ - cosφ > 0.98 → 切电容
│ - |U| > 1.05 p.u. → 切电容/投电抗
│ - 快变负荷 → SVG 指令 Q*
└─────────────────────────────────┘慢速环 (数周期):投切接触器式电容器组(步长 2
Mvar)快速环 (<10 ms):
SVG电流环实时注入 ±Q电压保护环:检测过压/三相不平衡,自动切除相应电容段
3.2 电容投切过渡抑制
串联 6 % 电抗器使谐振频率
f_r = \frac{f_0}{\sqrt{1 - k}}\approx 210~\text{Hz}远离 5、7 次 (250、350 Hz)
合闸利用 “零电压” 触发 (对于
TSC) 或同步条件 (真空断路器) 减小涌流
4 保护、监控与维护
在线监测
电容器介损 (tan δ)、套管局放
SVG IGBT 温度、电容 DC-Link 电压
35 kV 母线电压不平衡、谐波谱
5 经济与技术效果评估(示例)
6 小结
35 kV 母线常用 “固定 + 分级 + 动态 (SVG/SVC) + 吸收电抗” 的混合补偿方案,兼顾经济性与动态性能。
容量计算可用
Q_C = P(\tan\varphi_1-\tan\varphi_2)再按电压等级用
C = \dfrac{Q_C}{\omega U_{LL}^{2}}选定电容器。
串联电抗器(6 %–12 %)是 35 kV 高压电容补偿的必备配置,用来抑制谐振与涌流。
SVG 提供毫秒级动态无功与谐波治理,是应对冲击负荷、光伏/风电波动的重要手段。
控制策略以功率因数、母线电压双指标为核心,配合故障、谐波与不平衡保护,保障系统安全高效运行。
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途

