欧姆定律与功率

Ohms Law and Power

任何电气电路中电压 V、电流 I 和电阻 R 之间的关系最早由德国物理学家格奥尔格·欧姆发现。

格奥尔格·欧姆发现，在恒温条件下，通过固定线性电阻的电流与施加在其两端的电压成正比，同时与其电阻成反比。这种电压、电流和电阻之间的关系构成了欧姆定律的基础。但究竟什么是欧姆定律？它与电气电路有何关系？

欧姆定律是一个用于计算电气电路中电压、电流和电阻之间关系的公式，如下所示。

欧姆定律关系

Ohms Law Relationship

通过已知电压、电流或电阻中任意两个数值，我们可以使用欧姆定律求出第三个未知量。

因此，该欧姆定律公式可用于计算电路元件的阻值、电流强度、电源电压以及电路中的电压降。

欧姆定律在求解电气公式和计算时被广泛使用，因此准确理解并牢记基本的欧姆定律公式及其相互关系非常重要，必须清楚电压、电流与电阻三者是如何相互联动的。

求解电压 \displaystyle V

求解电流 \displaystyle I

求解电阻 \displaystyle R

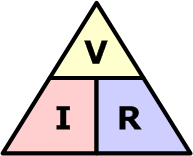
有时更容易通过图示来记忆欧姆定律的关系。 下图（欧姆定律三角图）将三个量叠加成一个三角形：顶点为电压 V，底边左侧为电流 I，底边右侧为电阻 R，此排列正对应各量在公式中的位置。

欧姆定律三角形

Ohms Law Triangle

对上面标准欧姆定律方程进行变换，可得到以下相同方程的不同形式：

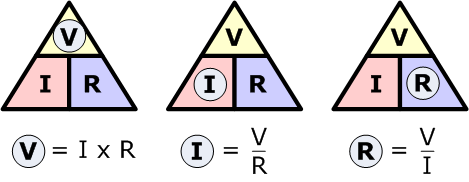
通过欧姆定律，我们可以看到：

• 施加 \displaystyle 1\,\mathrm{V} 电压于 \displaystyle 1\,\Omega 电阻上时，将产生 \displaystyle 1\,\mathrm{A} 电流流过；

• 电阻值越大，在相同电压下流过的电流就越小。

任何遵守“欧姆定律”——即流过其的电流与其两端电压成正比（\displaystyle I \propto V）——的电气器件或元件（如电阻器或电缆），称为欧姆性（Ohmic）器件；而不符合此规律的器件（如晶体管或二极管），则称为非欧姆性（Non-ohmic）器件。

电路中的电功率

Electrical Power in Circuits

电功率（P）是在电路中电能被吸收或产生的速率。能量源（如电压源）会输出功率，而连接的负载（如灯泡、加热器）则吸收功率并将其转换为热能或光能。功率的大小以瓦特（\mathrm W）为单位，常用前缀包括毫瓦（\mathrm{mW}=10^{-3}\,\mathrm W）和千瓦（\mathrm{kW}=10^3\,\mathrm W）。

功率的基本公式

To find the Electrical Power (P)

1. 电压乘以电流

   \boxed{P = V \times I} \quad P\;(\mathrm W)=V\;(\mathrm V)\times I\;(\mathrm A)

2. 电压平方除以电阻

   \boxed{P = \frac{V^2}{R}} \quad P\;(\mathrm W)=\frac{V^2\;(\mathrm V^2)}{R\;(\Omega)}

3. 电流平方乘以电阻

   \boxed{P = I^2 \times R} \quad P\;(\mathrm W)=I^2\;(\mathrm A^2)\times R\;(\Omega)

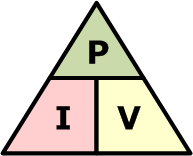
为了便于记忆，可将功率、电压和电流叠加成一个“功率三角图”：功率置于顶端，电流和电压置于底部，对应各自的公式位置。

功率三角形

The Power Triangle

再次，通过对上述基本欧姆定律功率方程进行变换，可得以下用于求解各个单独物理量的方程组合：

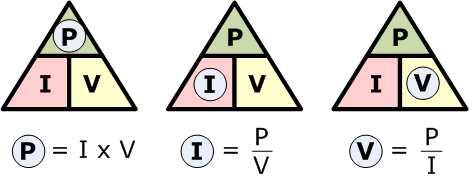
因此，我们可以看到在电路中有三种可能的电功率计算公式。如果使用任意一种公式计算出的功率为正值(+P)，则该元件会吸收功率，即消耗或使用功率；但如果计算出的功率为负值(−P)，则该元件会产生功率或输出功率，换句话说，它是电功率的源，例如电池和发电机。

电功率额定值

Electrical Power Rating

电气元件被赋予以瓦特为单位的“功率额定值”，用于表示该元件将电功率转换为其他形式的能量（如热能、光能或机械能）的最大速率。例如， \tfrac{1}{4}\mathrm W 的电阻、 100\mathrm W 的灯泡等。

电气设备会将一种形式的功率转换为另一种形式。例如，电动机将电能转换为机械力；发电机将机械力转换为电能；灯泡则将电能同时转换为光和热。

此外，我们现在知道功率的单位是瓦特（\mathrm W），但一些电气设备（如电动机）的额定功率仍使用旧制单位“马力”（\mathrm{hp}）。马力与瓦特之间的关系为：1\,\mathrm{hp} = 746\,\mathrm W，因此，例如一台两马力电动机的额定功率为 2 \times 746\,\mathrm W = 1492\,\mathrm W，即约 1.5\mathrm{kW}。

欧姆定律饼图

Ohms Law Pie Chart

为了帮助我们更深入地理解用于计算欧姆定律的各项数值之间的关系，我们可以将之前所有用于求取电压、电流、电阻以及功率的欧姆定律方程，浓缩为一个简单的欧姆定律饼图，以便在交流（AC）和直流（DC）电路及相应计算中使用，如下所示。

欧姆定律饼图

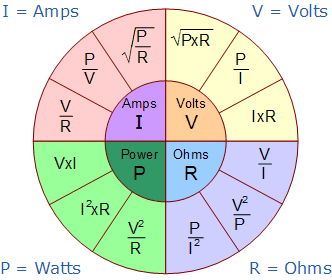
除了使用上面所示的欧姆定律饼图之外，我们还可以将各个欧姆定律方程放入一个简单的矩阵表格中，如下所示，以便在计算未知量时快速查阅。

欧姆定律矩阵表

欧姆定律练习1

对于下图所示电路，使用欧姆定律求出 电压 \,V、电流 \,I、电阻 \,R 与功率 \,P。

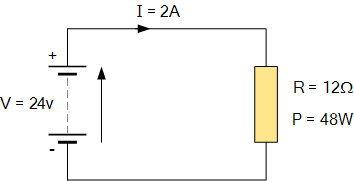
电压

电流

电阻

功率

电路中的功率只有在电压和电流同时存在时才会出现。例如，在开路条件下，虽然两端存在电压，但电流为零 \,(I=0)，因此 V \times 0 = 0,电路中消耗的功率也为零。

同样地，在短路条件下，虽然电路中有电流流动，但电压为零 \,(V=0)，因此 0 \times I = 0,电路中消耗的功率仍为零。

由于电功率等于 \,V \times I，无论电路是高压低流还是低压高流，其消耗的功率相同。通常，电功率以热能（如加热器）、机械功（如电动机）、辐射能（如灯）或存储能（如电池）的形式耗散或转换。

电路中的电能

Electrical Energy in Circuits

电能是做功的能力，做功或能量的单位是焦耳（ \mathrm J/joule）。电能等于功率与该功率持续时间的乘积。 因此，如果知道消耗的功率（以瓦特为单位）和使用时间（以秒为单位），就可以计算出以瓦特·秒（即焦耳）为单位的总能量。

用公式表示：

而由欧姆定律可知

故电能与功率的关系可写为：

其中

• E 单位为焦耳（\mathrm J），

• P 单位为瓦特（\mathrm W），

• t 单位为秒（\mathrm s）。

电功率也可定义为能量转移的速率。若以恒定速率在1秒内吸收或释放1焦耳功，则对应功率为1瓦特。因此有：

即1瓦特等于1焦耳每秒，电功率即是做功或能量转移的速率。

电功率和电能三角形

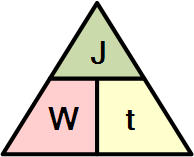
或者求得单独的变量：

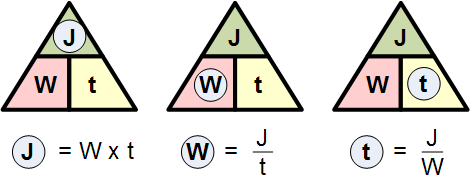
我们之前说过，电能的定义是瓦特·秒（ \mathrm{W\cdot s}）或焦耳（ \mathrm{J}）。虽然电能以焦耳为单位进行测量，但在计算元件消耗的能量时，其数值可能非常庞大。

例如，如果一个 100\,\mathrm{W} 的灯泡持续“开启” 24 小时，其消耗的能量为

因此常用千焦（ \mathrm{kJ}=10^3\,\mathrm{J}）或兆焦（ \mathrm{MJ}=10^6\,\mathrm{J}）来表示，在此例中即为 8.64\,\mathrm{MJ}.

但是，使用焦耳、千焦或兆焦来表示电能时，数字往往很大且零多，不便于理解，因此更常用千瓦·时来表示电能消耗。

如果以瓦特或千瓦（ 10^3\,\mathrm{W}）计量功率，并将时间以小时计算，则电能的单位为千瓦·时（ \mathrm{kW\cdot h}）。如此，上述 100\,\mathrm{W} 灯泡 24 小时的耗能可写为 100\,\mathrm{W} \times 24\,\mathrm{h} = 2400\,\mathrm{W\cdot h} = 2.4\,\mathrm{kW\cdot h},比起 8\,640\,000\,\mathrm{J} 更易理解。

1\,\mathrm{kW\cdot h} 即额定功率为 1000\,\mathrm{W} 的设备在 1\,\mathrm{h} 内消耗的电能，通常称为“度电”。这正是电能表所记录的，也是我们在收到电费账单时向供电商购买的电量。

千瓦·时是家用电表计算电能消耗并据此收费的标准单位。

例如，将一个功率为 1000\,\mathrm{W} 的电暖器开启 1\,\mathrm{h}，其消耗电量为 1\,\mathrm{kW\cdot h}.如果同时开启两个各 1000\,\mathrm{W} 的电暖器并持续 0.5\,\mathrm{h}，则总耗电量仍为 1000\,\mathrm{W} \times 0.5\,\mathrm{h} \times 2 = 1\,\mathrm{kW\cdot h}.

也就是说，以 1000\,\mathrm{W} 功率运行 1\,\mathrm{h} 与以 2000\,\mathrm{W} 功率运行 0.5\,\mathrm{h} 所消耗的电能相同。再如，要让一个 100\,\mathrm{W} 的灯泡消耗 1\,\mathrm{kW\cdot h}（一度电），需将其开启 10\,\mathrm{h}（即 10\times100=1000 瓦时，等于 1\,\mathrm{kW\cdot h}）。

既然我们已经了解了电压、电流与电阻在电路中的关系，在下一个关于直流电路的教程中，我们将介绍电气与电子工程中标准电气单位的使用，以便计算这些数值，并展示每个值如何用标准单位的倍数或分数来表示。

附录

物理学计量单位

一、SI 基本单位

二、SI 导出单位

力学

电磁学

热力学与光学

三、常用非SI单位

四、SI 单位前缀

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。