变压器负载
Transformer Loading
变压器可以在其次级绕组提供电压,但为了在其输入和输出之间传输电能,它们需要连接负载。
在之前的变压器教程中,我们假设变压器是理想的,即变压器的铁芯损耗和绕组的铜损耗都不存在。然而,在现实世界中,变压器在加载时总会有一些损耗,变压器处于“负载状态”时会产生这些损耗。那么,我们所说的变压器负载是什么意思呢?
首先,让我们看看当变压器处于空载no-load状态时会发生什么,即没有电气负载连接到其次级绕组,因此没有次级电流流动。
当变压器的次级绕组开路时,它被认为处于空载状态,换句话说,没有任何负载连接,变压器的负载为零。当一个交流正弦波电源连接到变压器的初级绕组时,由于初级电压的存在,会有一个小电流 I_{OPEN} 流经初级绕组。
由于次级电路开路,未连接负载,反向电动势与初级绕组的电阻共同作用,限制了这个初级电流的流动。显然,这个空载初级电流 I_o 必须足够大,以维持足够的磁场,从而产生所需的反向电动势。如下电路图:
空载条件下的变压器
Transformer “No-load” Condition
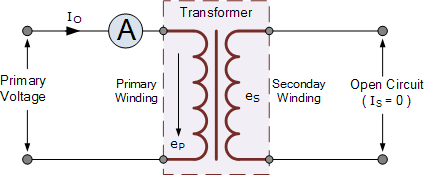
上面的电流表将显示即使次级电路开路,仍有少量电流流经初级绕组。这个空载初级电流由以下两个分量组成:
同相电流 I_E,它供应铁芯损耗(涡流损耗和滞后损耗)。
垂直于电压的小电流 I_M,它用来建立磁通。
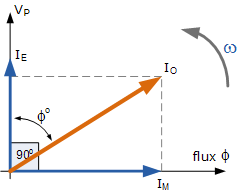
需要注意的是,这个空载初级电流 I_o 相比于变压器的正常满载电流非常小。此外,由于铁芯损耗以及初级绕组中的少量铜损耗,空载初级电流 I_o 并不会完全滞后于供电电压 V_p 90°(即 \cos \varphi = 0),而是存在一定的小相位差。
变压器负载示例 1
一台单相变压器的能量分量 I_E 为 2 安培,磁化分量 I_M 为 5 安培。计算空载电流 I_o 和相应的功率因数。
变压器空载
Transformer “On-load”
当电气负载连接到变压器的次级绕组,且变压器负载大于零时,次级绕组中会有电流流动并传递到负载。这个次级电流是由次级电压诱导产生的,而次级电压是由初级电流在铁芯中产生的磁通建立的。
次级电流 I_S 由负载的特性决定,产生了自感应的次级磁场 \Phi_S 在变压器的铁芯中,并且这个磁场的方向与主初级磁场 \Phi_P 恰好相反。这两个磁场相互对立,导致它们组合起来的磁场强度低于仅由初级绕组产生的单一磁场强度(当次级电路开路时)。
这个组合磁场降低了初级绕组的反向电动势,导致初级电流 I_P 稍微增加。初级电流将继续增加,直到铁芯的磁场恢复到原始强度。为了使变压器正常工作,初级和次级磁场之间必须始终保持平衡状态。这样,初级和次级的功率才能平衡并保持一致。考虑下图。
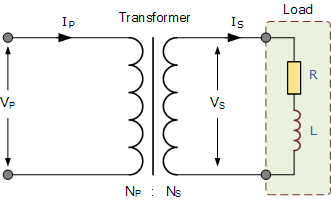
我们知道,变压器的匝比表明每个绕组中的总感应电压与该绕组中的匝数成正比,同时,变压器的输出功率和输入功率等于电压与电流的乘积 V \times I。因此:
但我们也知道,之前提到的变压器的电压比等于变压器的匝比,即:电压比 = 匝比。因此,变压器中的电压、电流和匝数之间的关系可以结合起来,公式如下:
变压器比率
Transformer Ratio
其中:
\frac{N_P}{N_S} = \frac{V_P}{V_S} 代表电压比
\frac{N_P}{N_S} = \frac{I_S}{I_P} 代表电流比
请注意,电流与电压和匝数成反比。这意味着,当次级绕组上加载变压器时,为了保持变压器绕组之间的功率平衡,如果电压被升高,则电流必须降低,反之亦然。换句话说,“高电压 — 低电流” 或 “低电压 — 高电流”。
由于变压器的比率是初级和次级绕组的匝数、电压和电流之间的关系,我们可以重新排列上述变压器比率方程,以求出任何未知电压(V)、电流(I)或匝数(N)的值,如下所示。
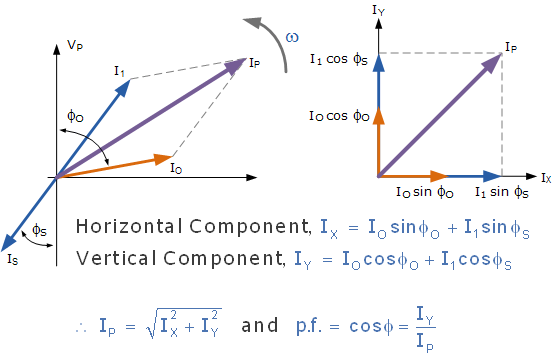
从电源中提取的初级绕组的总电流是空载电流 I_o 和次级变压器负载导致的额外电源电流 I_1 的矢量和,且该电流滞后于电源电压 \Phi 角度。我们可以通过相量图来表示这一关系。
变压器负载电流
Transformer Loading Current
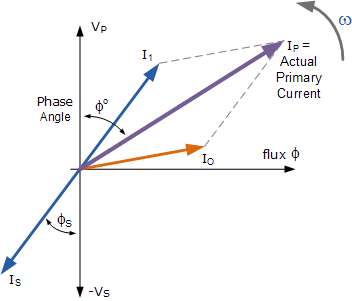
如果给定次级电流 I_S 和空载电流 I_o,我们可以通过以下方法计算初级电流 I_P。
变压器带载示例 2
一台单相变压器的初级绕组有 1000 匝,次级绕组有 200 匝。取自电源的变压器“空载”电流为 3 A,功率因数为 0.2 滞后。当次级电流为 280 A,功率因数为 0.8 滞后,承担变压器负载时,计算初级绕组电流 I_P 及其对应的功率因数 \varphi_P。
你可能已经注意到,初级电流的相位角 \varphi_P 与次级电流的相位角 \varphi_S 几乎相同。这是因为 3 A 的空载电流与初级绕组从电源取走的 56 A 相比非常小。
在实际应用中,变压器绕组具有电抗 X_L 和电阻 R 两种阻抗。这些阻抗在绘制相量图时需要考虑,因为它们会在绕组内部产生压降。绕组电阻引起的压降与因漏磁通产生的漏抗共同构成了变压器的内部阻抗,表示为:––––
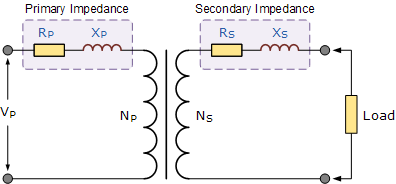
因此,变压器的初级绕组和次级绕组都具有电阻和电抗。有时,将所有这些阻抗值组合到变压器的同一侧,会使数学计算更加简便。
可以将初级阻抗移至次级侧,或将次级阻抗移至初级侧。这些组合后的 R 和 X_L 阻抗值称为“折算阻抗”或“反射值”。这里的目的是在计算中将变压器内部的阻抗汇总为一个折算后的 R 和 X_L 值,并应用于初级或次级侧,如下所示。
变压器阻抗组合
Combining Transformer Impedances
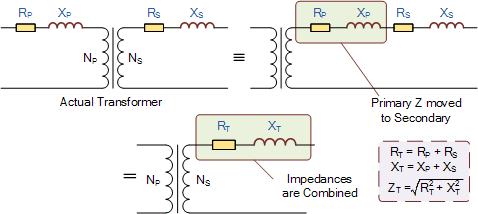
为了将电阻或电抗从变压器的一侧转换到另一侧,我们必须乘以或除以匝比的平方(即匝比的平方 \text{Turns Ratio}^2)。因此,将次级的阻抗(电阻和电抗)折算到初级侧时,我们需要乘以匝比的平方 N^2,而当将初级阻抗折算到次级侧时,则需要除以匝比的平方。因此,从次级到初级的折算会增加 R 和 X,而从初级到次级的折算则会按 N^2 的比例减少 R 和 X。
这种阻抗的折算(或反射)同样适用于连接负载的电阻和电抗。
举个例子,若次级的电阻为 2Ω,变压器的匝比为 8:1,那么折算到初级侧的电阻值为:
而若初级电阻为 2Ω,折算到次级侧的电阻值则为:
变压器电压调节
Transformer Voltage Regulation
变压器的电压调节定义为在变压器负载达到最大值(即满载时),当初级供电电压保持不变时,次级端电压的变化。电压调节决定了当负载过大导致变压器负载过高时,变压器内部发生的电压下降(或升高),这会影响变压器的性能和效率。
电压调节通常以电压的百分比(或单位值)表示。假设 E 代表空载时的次级电压,V 代表满载时的次级电压,则变压器的电压调节可以表示为:
例如,一个变压器在空载时提供 100 伏,而在满载时电压降至 95 伏,那么电压调节将是 5%。E - V 的值将取决于绕组的内部阻抗,其中包括其电阻 R 和更重要的交流电抗 X,电流以及相位角。
此外,电压调节通常随着负载功率因数的滞后性(感性)增加而增大。关于变压器负载的电压调节可以是正值或负值,即以空载电压为参考时,随着负载的增加,电压调节向下变化;或者以满载电压为参考时,随着负载的减少或移除,电压调节向上变化。
一般来说,当变压器负载较高时,核型变压器的电压调节性能不如壳型变压器。这是因为壳型变压器由于绕组的交错布置,具有更好的磁通分布。
在下一个关于变压器的教程中,我们将研究多绕组变压器,它具有多个初级绕组或多个次级绕组,并查看我们如何将两个或多个次级绕组连接在一起,以便为连接负载提供更多的电压或更多的电流。
变压器负载总结
在本节中,我们深入探讨了变压器在不同负载条件下的行为,特别是空载与满载状态下的性能变化,以及影响这些变化的关键因素。
1. 空载状态下的初级电流组成
在变压器空载时,初级电流 I_o 由两个主要分量组成:
同相电流 I_E:提供铁芯损耗(涡流损耗和滞后损耗)。
垂直于电压的小电流 I_M:用于建立磁通。
这两个分量的合成形成了空载初级电流 I_o,其计算公式为:
2. 负载状态下的电流与电压变化
当变压器连接负载时,次级电流 I_S 会在次级绕组中流动,进而在铁芯中产生与主磁场方向相反的自感应磁场 \Phi_S。这导致总磁场强度降低,从而减少了初级绕组的反向电动势,导致初级电流 I_P 略微增加。为了维持铁芯磁场的强度,初级电流继续增加,直到磁场恢复到原始强度。
3. 匝比与电压、电流的关系
变压器的匝比 n = \frac{N_P}{N_S} 决定了电压和电流的变化关系:
电压比: \frac{V_P}{V_S} = n
电流比: \frac{I_P}{I_S} = n
这意味着,电压与匝比成正比,而电流与匝比成反比。
4. 阻抗的折算
为了简化计算,可以将变压器的阻抗从一侧折算到另一侧。折算公式为:
从次级到初级: Z_P = Z_S \times n^2
从初级到次级: Z_S = Z_P / n^2
这使得在计算中可以将阻抗集中在一侧,简化分析过程。
5. 电压调节
电压调节定义为在满载条件下,次级端电压与空载时的电压之差与空载电压的比值。其计算公式为:
其中,E 为空载电压,V 为满载电压。电压调节通常以百分比表示,反映了变压器在负载变化时维持恒定电压的能力。
6. 实际应用中的考虑
在实际应用中,变压器的电压调节能力受到以下因素的影响:
负载类型:感性负载(如电动机)会导致更大的电压下降。
功率因数:低功率因数负载会导致更大的电压调节。
内部阻抗:绕组的电阻和电抗会引起压降,影响电压调节。
此外,变压器的类型(如壳型与核型)也会影响其电压调节性能。壳型变压器由于绕组的交错布置,通常具有更好的磁通分布,从而提供更好的电压调节性能。
7. 多绕组变压器
多绕组变压器具有多个初级或次级绕组,可以通过适当的连接方式,提供不同的电压或电流,以满足不同负载的需求。通过合理设计和连接,可以实现电压的升降或电流的分配,以适应多样化的负载要求。
附录
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

