并联电容器

Capacitors in Parallel

当电容器并联连接时，其两个端子都分别与另一电容器的对应端子相连。

并联连接的所有电容器两端所加的电压 (V_c) 相同。因此，并联电容器具有共同的电压，其表达式为：

在下图电路中，电容 C_1、C_2 和 C_3 均作为并联支路连接在 A 点和 B 点之间，如下所示。

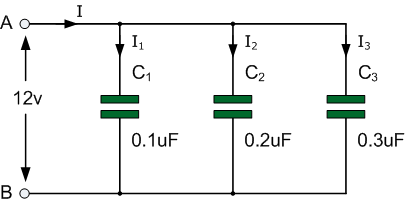
当电容器并联连接时，电路中的总电容或等效电容 C_T 等于所有单个电容器电容值之和。其原因在于电容 C_1 的上极板连接到 C_2 的上极板，后者又连接到 C_3 的上极板，以此类推。

同理，所有电容器的下极板也相互连接。这样就相当于三组极板相互贴合，形成了一块更大的单一极板，从而增大了有效极板面积（单位：\mathrm{m}^2）。

由于电容与极板面积成正比（C = \varepsilon \dfrac{A}{d}），并联组合的电容值也随之增大。因此，并联电容器的等效电容可表示为各电容器电容之和。你可能已经注意到，并联电容的总电容计算方式与串联电阻的总电阻计算方式相同。

流经每个电容器的电流与加在其上的电压有关。对上述电路应用基尔霍夫电流定律（KCL），我们得到：

还可以改写成:

那么我们可以将电路的总电容 C_T 定义为所有单个电容值之和，从而得到并联电容器的一般方程：

并联电容器方程

Parallel Capacitors Equation

当将电容器并联相加时，必须先将它们全部换算到相同的电容单位（例如 \mu\mathrm{F}、nF 或 pF）。此外，我们可以看到流过总电容值 C_T 的电流与总电路电流 i_T 相同。

我们也可以使用电荷公式

根据电容器极板上的电荷来定义并联电路的总电容。所有电容器极板上存储的总电荷 Q_T 等于各电容器存储电荷之和，因此，

由于并联电容器的电压 V 相同，我们可以将上述方程的两边同时除以电压，仅剩下电容值；通过简单地将各个电容值相加即可得到总电容 C_T。

此外，该方程与任何支路中并联电容器的数量无关，因此对于任意数量的 N 个并联电容器都可以使用此公式，因为这只是一个简单的加法过程。

教程示例 1

因此，从上述示例中取三电容值，可计算电路等效总电容 C_T 为：

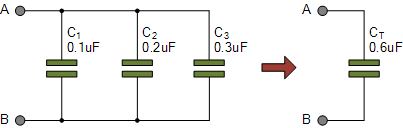
一个要点需铭记：在并联电容电路中，任何两个或以上电容器并联时的总电容 C_T 必然大于组中最大电容的数值，因为我们是将各电容值相加。因此在上例中， C_T=0.6\,\mu\mathrm{F}，而并联组合中最大的单个电容仅为 0.3\,\mu\mathrm{F}。

当连接四个、五个、六个或更多电容器时，电路总电容 C_T 仍为所有单个电容之和；如我们所知，并联电路的总电容始终大于其中最大电容的值。

这是因为我们有效地增加了极板的总表面积。若使用两个相同电容器，则极板面积翻倍，组合电容也随之翻倍；以此类推。

教程示例 2

计算以下电容器并联时的总电容（单位：微法拉， \mu\mathrm{F}）：

a) 两个各为 47\,\mathrm{nF} 的电容器

b) 一个 470\,\mathrm{nF} 的电容器与一个 1\,\mu\mathrm{F} 的电容器并联

因此

由此可见，含有两个或更多并联电容器的电路的总电容 C_T 等于各电容值之和，这是由于有效极板面积增加所致。

在下一个关于电容器的教程中，我们将探讨电容器的串联连接以及该组合对电路总电容、电压和电流的影响。

附录

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。