串联电容器 Capacitors in Series
当多个电容器首尾相连成一条直线时,就称这些电容器为串联连接。
在串联连接中,流经各电容器的充电电流 i_C 是相同的,因为电流只有一条路径可走。
因此,串联电容器中的电流相等,即
i_T = i_1 = i_2 = i_3 = \dots
每只电容器的极板上所存储的电荷量 Q 也相同,与其电容量无关。这是因为任一电容器极板上的电荷必须来自其相邻电容器的极板。因此,串联的电容器必定具有相同的电荷。
Q_T = Q_1 = Q_2 = Q_3 = \dots
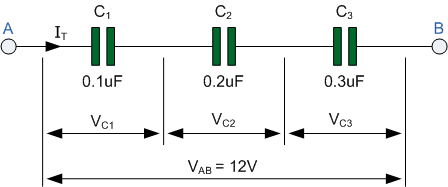
下图所示电路中,三只电容器 C_1、C_2 和 C_3 首尾相连,构成一条跨接在 A、B 点之间的串联支路。
Capacitors in a Series Connection
在前面的并联电路中,我们看到电路的总电容 C_T 等于所有单个电容器之和。然而,在串联连接的电路中,总电容
C_T 的计算方式则不同。
在上图的串联电路中,第一个电容器 C_1 的右极板与第二个电容器 C_2 的左极板相连,而 C_2 的右极板又与第三个电容器 C_3 的左极板相连。对于直流电路而言,这种串联连接意味着电容器 C_2 实际上被隔离出了电路。
其结果是,有效极板面积减少到串联链中最小的单个电容值 。因此,各电容器两端的电压降将根据它们各自的电容值而有所不同。
然后,通过对上述电路应用基尔霍夫电压定律(KVL),我们得到:
V_{AB} = V_{C1} + V_{C2} + V_{C3} = 12\,\mathrm{V},
其中
V_{C1} = \frac{Q_T}{C_1},\quad V_{C2} = \frac{Q_T}{C_2},\quad V_{C3} = \frac{Q_T}{C_3}.
由于
Q = C \cdot V
重排得
V = \frac{Q}{C},
将 \displaystyle \frac{Q}{C} 代入上述 KVL 方程中每个电容的电压 V_C ,可得:
V_{AB} = \frac{Q_T}{C_T} = \frac{Q_T}{C_1} + \frac{Q_T}{C_2} + \frac{Q_T}{C_3}.
两边同时除以 Q_T ,得到串联电容器的公式:
串联电容公式 Series Capacitors Equation
\frac{1}{C_T} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \dots.
在串联连接中,各电容器的倒数 \frac{1}{C} 相加(类似于电阻并联),而不是直接相加电容值。因此,总电容等于各单个电容倒数之和的倒数。
教程示例 1 取上述示例中三个电容器的数值,我们可以计算它们串联后的等效总电容 C_T 为:
\frac{1}{C_T} \;=\;\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}
\frac{1}{C_T} =\Bigl(\frac{1}{0.1\,\mu\mathrm F}+\frac{1}{0.2\,\mu\mathrm F}+\frac{1}{0.3\,\mu\mathrm F}\Bigr) =18.33\times10^6\;\mathrm F^{-1}
\therefore\quad C_T=\frac{1}{18.33\times10^6} =0.055\,\mu\mathrm F
串联连接的电容器有一点要记住:任何数量的电容器串联时,总电容 C_T 必然小于串联链中最小的电容值 。在上例中,总电容 C_T 计算为 0.055\,\mu\mathrm F ,而串联链中最小的电容仅为 0.1\mu\mathrm F
这种倒数相加的方法可用于计算任意多个电容器的串联。当只有两个电容器串联时,可以使用更简单快捷的公式,其表达式为:
C_T = \frac{C_1\,C_2}{C_1 + C_2}.
如果两个串联的电容器相等且具有相同的电容值,即:
C_1 = C_2 = C,
那么上述公式可以进一步简化为:
C_T = \frac{C_1\,C_2}{C_1 + C_2} = \frac{C\cdot C}{C + C} = \frac{C^2}{2C} = \frac{C}{2}.
那么我们可以看到,当且仅当两个串联电容器相同且电容值相等时,总电容 C_T 恰好等于电容值 C 的一半,也即:
C_T = \frac{C}{2}.
对于串联连接的电阻,所有电压降之和等于施加电压 V_S (基尔霍夫电压定律),串联电容器亦是如此。
在串联电容器中,由于电源频率的作用,电容器表现出电抗,其阻抗会在每只电容器上产生电压降,因此串联电容器构成了一个电容分压网络。
结果是,电阻分压公式同样可用于求解两只串联电容器的各自电压。那么:
V_{C_X} \;=\; \frac{C_T}{C_X}\,V_S
其中:
C_X 是所讨论电容器的电容;
V_S 是加在串联链上的电源电压;
V_{C_X} 是目标电容器两端的电压降。
教程示例 2 在 12 V 交流电源下,求以下两组串联电容的等效电容及各电容器的有效电压降:
a) 两只电容各为 47\,\mathrm{nF}
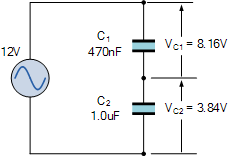
b) 一只电容为 470\,\mathrm{nF} 串联一只电容为 1\,\mu\mathrm{F}
a) 等值串联电容 Total Equal Capacitance
C_T = \frac{C_1\,C_2}{C_1 + C_2} = \frac{47\,\mathrm{nF}\times47\,\mathrm{nF}}{47\,\mathrm{nF}+47\,\mathrm{nF}} =23.5\,\mathrm{nF}
各电容电压降:
V_{C1}=V_{C2} =\frac{C_T}{C_1}\,V_S =\frac{23.5\,\mathrm{nF}}{47\,\mathrm{nF}}\times12\,\mathrm{V} =6\,\mathrm{V}
b) 不等值串联电容 Total Unequal Capacitance
C_T = \frac{C_1\,C_2}{C_1 + C_2} = \frac{470\,\mathrm{nF}\times1\,\mu\mathrm{F}}{470\,\mathrm{nF}+1\,\mu\mathrm{F}} =320\,\mathrm{nF}
各电容电压降:
V_{C1} =\frac{C_T}{C_1}\,V_S =\frac{320\,\mathrm{nF}}{470\,\mathrm{nF}}\times12\,\mathrm{V} \approx8.16\,\mathrm{V}
V_{C2} =\frac{C_T}{C_2}\,V_S =\frac{320\,\mathrm{nF}}{1\,\mu\mathrm{F}}\times12\,\mathrm{V} \approx3.84\,\mathrm{V}
由于基尔霍夫电压定律(KVL)适用于该串联电路及所有串联电路,各电容器两端电压降之和必等于电源电压 V_S 。因此:
8.16 + 3.84 = 12\,\mathrm{V}.
此外,如果电容值相同(如第一个示例中的 47\,\mathrm{nF} ),则电源电压会均匀地分配到每只电容器两端。这是因为串联链中每只电容器所带的电荷量相等且精确相同(Q = C \times V = 0.564\,\mu\mathrm{C} ),故每只电容器承受电压为总电压的一半(对于多于两只电容器的情况,则为相应的百分比分压)。
而当串联电容值不同时,电容值较大的那只承受较低电压,电容值较小的那只承受较高电压。在上述第二个示例中,它们分别为 3.84\,\mathrm{V} 和 8.16\,\mathrm{V} 。这种电压差异使各电容器能够在其极板上保持相同的电荷量 Q。
\begin{align} Q_{C1}&=V_{C1}\times C_{1}=8.16\,\mathrm V\times 470\,\mathrm{nF}=3.84\,\mu\mathrm C, \\ Q_{C2}&=V_{C2}\times C_{2}=3.84\,\mathrm V\times 1\,\mu\mathrm F=3.84\,\mu\mathrm C. \end{align}
注意,串联连接的两只电容器上的电压降比率将始终保持不变,无论电源频率如何,因为它们的容抗 X_C 会按比例保持相同。
因此,即使将电源频率从 100\,\mathrm{Hz} 提高到 100\,\mathrm{kHz} ,在我们上面的简单示例中,两个电压降 8.16\,\mathrm V 和 3.84\,\mathrm V 仍然不变。
尽管在不同电容值下各电容器两端的电压降会不同,但由于串联电路中流经的电流相同——所有电容器都被相同数量的电子所充电——所以各极板上的库仑电荷量 Q 是相等的。
换言之,如果各电容器极板上的电荷量相同( Q 保持不变),那么当电容减小时,由于电荷相对于电容而言较大,极板电压降就会增大;同理,较大的电容由于电荷相对于电容而言较小,其极板电压降就会减小。
教程总结 然后,总结如下:
含有串联电容器的电路的总电容 C_T 等于各单个电容倒数之和的倒数:
\frac{1}{C_T} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + \dots
对于串联连接的电容器,所有电容器的充电电流相同:
i_T = i_1 = i_2 = i_3 = \dots
串联的两只或多只电容器极板上的库仑电荷量 Q 恒相等。
由于电荷 Q 相同且恒定,电容器两端的电压降仅由电容值决定:
V = \frac{Q}{C}.
当电容值较小时,电压降会增大;当电容值较大时,电压降会减小。
附录 电力场景下的串联电容 应用场景
作用
说明
高压电容器组
构建高耐压电容器
单个电容器的额定电压通常在几百伏到几千伏之间,若要在数十千伏甚至上百千伏的系统中使用,就必须将多只同容量电容器串联,并在两端并联均压电阻/均压电容,以保证各只电容器分担相同电压。常用于静止无功补偿(SVC)、静止同步补偿(STATCOM)等装置中的主回路电容器。
电容式电压互感器 (CCVT)
电压分压与谐波滤波
CCVT 中常用两级或多级串联电容器构成初级分压器,不仅分压比大,还兼具对高次谐波的滤波作用,下游再加补偿电感或阻尼网络,得到准确的二次电压波形,供保护和测量使用。
直流母线电容串联
实现高压直流母线
在风电/光伏逆变器或 HVDC 换流装置的直流侧,需要数百到上千伏的母线电压。常将多组低压电解或薄膜电容串联,并加均压电阻,构成直流中间环节的储能与滤波元件。
谐振试验与滤波
构造谐振回路/滤除谐波
高压谐振试验装置中,为获得特定的谐振频率会将电容器与电抗器串联;在电力系统谐波治理中,也可将几只电容串联后并联电抗,针对某次谐波形成低阻抗通路,将谐波“旁路”至地/中性点。
EMI/EMC 安规滤波器
差模电容与安全等级
在电网侧 EMI 滤波 X 电容多为多只电容串联,以满足更高的介质耐压要求;串联间通常并联均压电阻,确保每只电容分担相同直流偏置电压,并通过金属外壳实现安全接地。
单词表 English Term
中文翻译
High-voltage capacitor bank
高压电容器组
Voltage rating
电压耐压
Balancing resistor
均压电阻
Balancing capacitor
均压电容
CCVT (Capacitor Voltage Transformer)
电容式电压互感器
Voltage divider
分压器
Harmonic filtering
谐波滤波
DC bus capacitor
直流母线电容
Wind/PV inverter
风电/光伏逆变器
HVDC converter
HVDC 换流装置
SVC (Static Var Compensator)
静止无功补偿装置(SVC)
STATCOM (Static Synchronous Compensator)
静止同步补偿装置(STATCOM)
EMI/EMC safety filter
EMI/EMC 安规滤波器
X capacitor
X 电容
ESR (Equivalent Series Resistance)
等效串联电阻(ESR)
Damping network
阻尼网络
Capacitive reactance (X_C)
容抗(X_C)
Mid-point voltage
中点电压
Resonant test
谐振试验
Energy storage
储能
声明 本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。