磁场中的能量
Energy in a Magnetic Field
线圈中储存的能量取决于其能量密度,而能量密度与磁场强度的平方 \propto H^2 成正比,并分布在环绕线圈的空间体积中。
磁场中是否存在能量
Is There Energy in a Magnetic Field
磁性的效应通常通过磁场的存在来描述,磁场中储存的能量取决于若干关键因素,其中包括磁场强度 H 以及产生该磁场的电流 I,特别是在绕组线圈和螺线管中。
每一磁场都包含一定形式的能量,我们通常将其称为磁性能量 W_m。磁场中储能的原理是物理学的基本概念之一,并在电磁学与电子技术等诸多领域中得到广泛应用。那么,磁性是否真能被视作一种能量形式呢?
正如我们所知,磁场是分布在磁性材料周围开放空间中的区域。它通常由闭合的力线来表征,这些力线从北极端出发,经空间再回到南极端。磁场在磁性材料内部以及极点附近最为强烈;随着距离的增加,磁场强度逐渐衰减。
我们通常通过磁场的强度和方向来描述其效应。磁场既可由永久磁体产生,也可由导线上流动的电流所生成。
对于电磁铁electromagnet而言,当导体被绕制成具有大量匝数的线圈时,所产生的磁场尤为强大。因此,一根长直线圈(螺线管)能够产生与永久磁铁类似的近似均匀磁场,如下图所示。
磁体周围的磁场
Magnetic Field Around Magnets
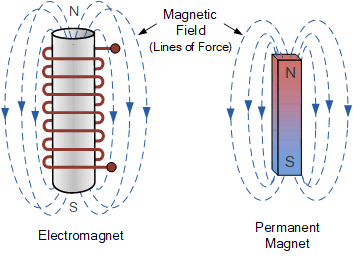
磁力线表示绕永久磁体或电磁铁产生的磁通 \Phi 的流向。每条磁通线都形成一个闭合回路,如虚线所示,且彼此永不相交。磁场强度 H 定义为:
其中, B 为磁通密度, \mu_0 为真空磁导率。
磁场中的能量如何储存
How is Energy Stored in a Magnetic Field 所有磁场都储存一定的能量,这些能量可来源于永久磁体或电磁铁。由硬质合金制成的永久磁体会在其周围空间中产生并保持恒定的磁场;而由导线绕制成线圈的电磁铁,则根据线圈的匝数和所承载的电流大小,在其周围产生可变的磁场。电磁线圈(称为螺线管)在实际应用中具有极其广泛的用途。
要描述因电流作用而在绕组线圈内部形成的磁场的能量密度,需要考虑一个具有 N 匝的电感器,因为电感器具有储能能力。
电感器是一种电子无源器件,它本身不产生能量,而是将能量以磁性能量的形式储存在其线圈中。因此,当电流流经线圈时,所储存的能量称为磁性能量 W_m。
电感器磁场中的能量可与产生或改变其磁场所做的功相联系,即电压源为维持线圈内电流所做的功。所储能量及磁场强度取决于电流大小,以及电感器的几何形状和物理特性。
由于电感器磁场中的能量与最初产生该磁场的电流大小有关,而与维持该电流无关。为强制电流通过电感器线圈所做的功(以瓦特为单位)表示为:
电感器两端的电压为:
V_L = L \frac{dI}{dt}其中 \displaystyle \frac{dI}{dt} 是流经电感器的电流变化率, L 表示自感量。
电源向电感器提供的瞬时功率 P 为:
P = V_L \times I = L\,I\,\frac{dI}{dt}\quad\text{瓦特}
由于电感具有将能量储存在磁场中的能力,将上述功率公式在电流以 \tfrac{V}{L} 安培每秒的速率从 0 匀速增至 I 的时间区间 [0,t] 上积分,可得:
因此,当电流 I 流过电感器时,其磁场中可储存的总磁性能量 W_m 表示为:
电感器中储存的能量
其中,
L 为电感器的自感量,单位为亨利(\mathrm{H});
I 为电流,单位为安培(\mathrm{A})。
注意,系数 \tfrac12 来源于对向电感器输送的功率进行积分时,平均电流为 \tfrac{I}{2}。我们还可以看到,储存的能量与电流的平方 I^2 成正比——电流加倍时,储能增加到原来的四倍。
此外,更大的电感量意味着在相同电流下可以储存更多能量。自感量取决于线圈的匝数、横截面积和线圈长度。
教程示例 1
计算一个电感量为 2\,\mathrm{H} 的绕组线圈在电流达到最大值 3\,\mathrm{A} 时,其磁场中储存的能量:
这意味着该线圈在其磁场中储存了 9 焦耳的能量。
利用磁场强度计算能量密度
Using the Magnetic Field Strength
使用磁场强度 我们也可以使用线圈或螺线管的磁通密度 B 来计算均匀磁场中的能量密度(每立方米的能量),因为周围磁场越强,所储存的能量越多。磁场的单位体积能量密度有时更为重要,因为它与磁场强度(H)的平方成正比。
我们之前看到,用电流和自感量给出的磁场总能量为:
但就线圈、螺线管或电感器的电感而言,还可以根据其物理特性和磁场特性以多种方式来表示。
对于一个螺线管,其电感 L 可表示为:
其中:
\mu_0 是磁常数,即真空磁导率 \mu_0 = 4\pi\times10^{-7}\,\mathrm{H/m};
N 是单位长度的匝数;
A 是螺线管的横截面积;
\ell 是螺线管的长度。
这表明电感 L 取决于线圈的物理特性,并且与匝数 N 的平方成正比。
在螺线管线圈中,内部磁通密度 B 与电流 I 的关系为:
其中:
B 是磁通密度;
N 是单位长度的匝数;
I 是电流。
由上述磁通密度 B 的公式,如果我们将电流 I 用 B 表示,则得到:
现在,将上述 I 和 L 代入原始的储能公式中,可得:
这个方程表示储存的能量。然而,螺线管(电感器)磁场所占据的体积为 V = A\ell,因此可以求得环绕螺线管(电感器)磁场的单位体积磁性能量密度。
表示单位体积磁性能量密度
Expressing Magnetic Energy per Unit Volume
总能量 W_m 分布在螺线管的体积 V = A\ell 上。为了求得能量密度 U_B(单位体积的能量),我们必须将总能量除以体积:
因此,在真空中磁场任一点的能量密度可以简化为一个更通用的公式:
磁场中的能量密度
Energy Density in a Magnetic Field
上述用于描述磁性材料场的能量密度方程表明,分布在螺线管体积上的单位\mathrm{m}^3空间内储存的能量与磁通密度 B 的平方成正比,并与介质的磁导率 \mu_0(对于真空)成反比。
当磁场形状不均匀时,或在磁性材料周围任意存在磁场的空间区域中,该表达式同样成立。
教程示例 2
一个螺线管线圈的电感量为 2.0\;\mathrm{mH}。计算:
(a) 场中储存的磁性能量
(b) 磁场中的能量密度 螺线管总体积为 0.16\;\mathrm{mm}^{3},须先将其换算为 \mathrm{m}^{3}:
能量密度
(c) 螺线管内部的磁通密度 真空磁导率 \mu_{0}=4\pi\times10^{-7}\;\mathrm{H/m}。由
磁性能量存储在哪里
Where is the Magnetic Energy Stored
磁性能量分布在磁场存在的整个空间体积内。对于单位长度有 N 匝、长度为 \ell、截面积为 A 的螺线管,该体积可简洁表示为:
当磁场均匀时,磁场在铁芯内部最为强烈,因此大部分能量储存在铁芯内。如果线圈为无磁性材料(气芯电感器),则能量储存在磁通路径中人为引入的气隙和周围空间中。
由于磁性能量最好由其单位体积能量密度来描述(即能量 per 单位体积),因此它主要储存在环绕线圈的空间中(对于螺线管而言,主要是在线圈内部)。在线圈内部,磁力线平行于线圈轴向分布,能量就储存在这些力线所占据的空间里。
在本教程中我们看到,电感器和绕组线圈能够将能量以磁性能量的形式储存在其环绕并存在于铁芯内的磁场中。该磁性能量定义为:
能量分布在磁场存在的所有空间体积内,通常在螺线管内部的浓度最高。
当电流增加时,电感器会在其磁场中储存能量;当电流减小或中断时,磁场崩塌,释放所储存的能量。
附录
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

