在交流电路中的电容

Capacitance in AC Circuits

当电容器连接到正弦电源时，由于电源频率和电容器容量的影响，会产生一种称为容性电抗（capacitive reactance）的效应。

在交流电路中，电容器电流随时间变化，并相对于电源电压超前 90^\circ ，这种现象就称为容性电抗。

当电容器接在直流（DC）电源上时，其两极板会充电直到电容器两端的电压等于外加电压。只要外加电压保持不变，电容器就会一直保持这一电荷，充当一种临时的储能装置。

在这个充电过程中，会有电流 i 流入电容器，使其极板开始存储静电电荷。由于极板间的静电场会以与极板上电荷变化率相同的速率来抵抗电压变化，电容器的充电电流并非瞬时或线性的：当电容器极板未充电时，充电电流最大；随着极板电荷的累积，电流呈指数方式减小，直到电容器完全充电为止。

电容器存储电荷的能力称为电容 C。因此，电容器的充电电流可表示为：

一旦电容器“充满”电荷，就阻止更多电子流入极板；而当我们将直流电源替换为交流电源时，电容器便会以电源频率交替进行充放电，从而使得交流电路中的电容效应随着频率的变化而变化。

因为电子流入极板的多少正比于极板电压的变化率，电容器在电压不断随时间变化（如交流信号）时容易通过电流；但是在电压保持恒定（如直流信号）时则不易导通。如下图所示：

交流电容器电路

AC Capacitor Circuit

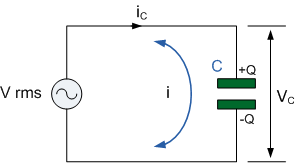
在上图的纯电容电路中，电容器直接并联于交流电源电压。当电源电压升高和降低时，电容器便相应地充电和放电。我们知道，充电电流与极板电压的变化率成正比，当电源电压沿正半周交越到负半周（或反之）时，即在正弦波的 0^\circ 和 180^\circ 点处，电压的变化率达到最大值。

因此，当交流正弦波交越到最大正峰（ +V_{\mathrm{MAX}} ）和最小负峰（ -V_{\mathrm{MAX}} ）时，电压变化率最小。在这两个位置，正弦电压为恒定值，其变化率为零，即

导致电容器内的电流变化也为零。因此，当 \frac{dv}{dt} = 0 时，电容器相当于开路，即

如下面所示。

交流电容器相量图

AC Capacitor Phasor Diagram

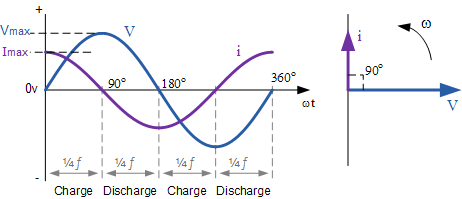
在 0^\circ 时，电源电压的变化率向正方向增加，导致在该瞬时有最大充电电流。随着所加电压在 90^\circ 处达到最大峰值，在这极短的瞬间，电源电压既不升高也不降低，因此电路中无电流流动。

当所加电压开始以负斜率下降至 180^\circ 时，电容器便向负方向放电。在 180^\circ 点，电压的变化率再次达到最大值，因此此刻流过的电流也达到最大，依此循环。

由此可见，对于交流电路中的电容器，当所加电压处于最大值时，瞬时电流为最小或零；而当所加电压为零时，瞬时电流则为最大或峰值。

从上述波形可看到，电流相对于电压超前了 \tfrac{1}{4} 周期，即 90^\circ，如相量图所示。因此，在纯电容电路中，交流电压相对于电流滞后 90^\circ。

我们知道，流经电容器的交流电流与所加电压的变化率相对应，但与其方向相反。就像电阻那样，电容器也会对电流流动产生某种阻碍。在交流电路中，这种阻碍称为电抗Reactance；对于电容器而言，专门称作容性电抗Capacitive Reactance。因此，交流电路中的电容器会受到容性电抗的影响。

交流电路中的电容——电抗

Capacitance in AC Circuits – Reactance

在纯电容电路中，容性电抗仅是对交流电路中电流流动的阻碍。像电阻一样，电抗的单位也是欧姆（\Omega），但用符号 X 来区别于纯电阻值。由于电抗既可以应用于电感器也可以应用于电容器，当用于电容器时，更常称为“容性电抗”。

对于交流电路中的电容器，容性电抗的符号为 X_C。因此，我们可以说，容性电抗是一个随频率变化的电容器“电阻”值。此外，容性电抗取决于电容器的电容（单位：法拉， \mathrm{F}）以及交流波形的频率，其定义公式如下：

容性电抗

其中： f 的单位为赫兹（ \mathrm{Hz}），C 的单位为法拉（ \mathrm{F}）。 2\pi f 也可统一表示为希腊字母 \omega，用于表示角频率。

从上述容性电抗公式可见，若增大频率或电容值，容性电抗会减小。当频率趋于无穷大时，电容器的电抗趋于零，表现如理想导体。

而当频率趋于零（直流）时，电容器的电抗会增大至无穷大，表现如极大电阻。因此，对于任意给定的电容值，容性电抗与频率“成反比”，如下所示：

容性电抗随频率变化

Capacitive Reactance against Frequency

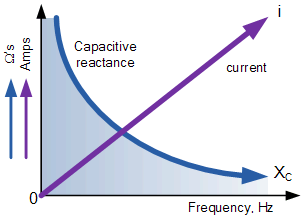
电容器的容性电抗 X_C 随频率 f 增大而减小，因此 X_C 与 f 成反比。

对电流的阻碍——即极板上的静电电荷（其交流电容值）保持不变，因为电容器在每个半周期内更容易完全吸收极板上电荷的变化。

此外，随着频率 f 的增加，流经电容器的电流 i 也会增大，因为极板间电压的变化率 \frac{dv}{dt} 增大。

由此可见，在直流（ f=0）时，电容器的容性电抗 X_C\to\infty（开路,隔直流）；在极高频率（ f\to\infty）时， X_C\to0（短路，通交流）。

交流电路中的电容示例 1

题目： 在 880 V、60 Hz 的交流电源下，将一个 4 μF 的电容器并联于电源，求流过电容器的有效值电流。

解答：

容性电抗定义为

电容器的有效值电流为

在交流电路中，流过电容器的正弦电流相对于电压超前 90^\circ，且随着电容器不断充放电，该电流随频率变化。电容器的交流阻抗称为电抗（Reactance），对于电容器专称“容性电抗” X_C。

交流电路中的电容 示例 2

题目： 当一个平行板电容器接到 60 Hz 的交流电源时，测得其容性电抗为 390 Ω。求该电容器的电容量，单位为微法拉（μF）。

解答：

根据容性电抗公式：

将已知数值代入：

该容性电抗与频率成反比（X_C\propto\frac{1}{f}），并对电容性交流电路中的电流流动产生阻碍，正如我们在“交流理论”部分的“交流电容”教程中所看到的那样。

附录

单词表

声明

本文翻译自 electronics-tutorials

本文仅供学习，禁止用于任何的商业用途。