变压器电压调节
Transformer Voltage Regulation
变压器电压调节是指变压器输出端电压相对于其空载值,因连接负载电流变化而向上或向下波动的比例或百分比值。
什么是变压器调压?
What is Transformer Regulation?
电压调压是衡量变压器在不同负载条件下维持恒定二次电压能力的指标,因为输出二次电压可能并非理想预期值。
当变压器的一次绕组通电时,会按照变压器的匝比( \mathrm{TR})在二次侧产生相应的电压和电流。如果某单相变压器的降压匝比为 2:1,并在高压一次绕组上施加 240\,\mathrm{V},理想情况下我们期望在二次绕组的输出端看到 120\,\mathrm{VAC}。
然而在现实中,并非总是如此。作为一个绕组磁电路,所有变压器都会遭受由 I^2R 铜损和磁芯损耗组成的损耗,这会使理想二次电压降低几个百分点,比如降至 117\,\mathrm{VAC},这是正常现象。
但在变压器满载供电时,还有另一项与变压器(及电机)相关的因素也会影响二次电压,这就是所谓的“调压(regulation)”。
Transformer 电压调节
Transformer Voltage Regulation
单相变压器的电压调节是指在不同二次负载条件下,其二次端电压相对于原始空载电压的百分比(或标幺值)变化。
换言之,调压反映了由于变压器所连接负载的变化而在变压器内部产生的二次端电压波动,这会影响其性能和效率;如果损耗过大,二次电压就会过低。
空载条件:当二次绕组开路,输出端无闭合回路,故无输出负载电流(I_L=0),此时变压器表现为单个高自感绕组。空载二次电压由一次电压和变压器匝比共同决定。
负载条件:当在二次绕组上接入简单负载阻抗时,会有任意功率因数的二次电流 I_L 流经变压器绕组。绕组的内部电阻和漏抗引起的电压降会导致输出端电压发生变化。
对于一次电压恒定的情况,当二次端电压从空载( I_L=0 开路)变化到满载(I_L=I_{\mathrm{MAX}})时,其电压调节量可表示为:
以分数变化表示的变压器电压调节
Transformer Voltage Regulation as a Fractional Change
请注意,当将此电压调节表示为空载端电压的分数变化或单位变化时,可定义为两种方式:降调(Regdown)和升调(Regup)。
也就是说,当负载接入二次输出端时,端电压下降;当负载移除时,二次端电压上升。因此,变压器的调压取决于所采用的参考电压值——负载值还是空载值。
我们还可以将变压器电压调节表示为空载条件和满载条件之间的百分比变化,如下所示:
变压器电压调节的百分比变化
Transformer Voltage Regulation as a Percentage Change
例如,假设我们有一台单相变压器,其开路(空载)端电压为 100\ \mathrm{V},当施加阻性负载后,端电压下降到 95\ \mathrm{V}。该变压器的电压调节因此为:
因此,变压器的电压调节可以表示为单位变化值(本例中为 0.05),也可以表示为相对于原始空载电压的百分比变化值(本例中为 5\%)。
变压器电压调节示例 1
一台 500 VA、匝比 10 : 1 的单相降压变压器一次绕组由恒定 240 V_{\mathrm{rms}} 电源供电。当其二次侧连接阻抗 Z_S = 1.1\,\Omega 时,求该变压器的百分比调压。
已知数据:
计算过程:
空载二次电压
\frac{V_S}{V_P} = \frac{N_S}{N_P} \quad\Longrightarrow\quad V_{S(\mathrm{空载})} = V_P \times \frac{N_S}{N_P} = 240 \times \frac{1}{10} = 24\ \mathrm{V}满载二次电压
P = \frac{V_S^2}{Z} \quad\Longrightarrow\quad V_{S(\mathrm{满载})} = \sqrt{P \times Z} = \sqrt{500 \times 1.1} = 23.45\ \mathrm{V}百分比调压
\%\mathrm{Reg} = \frac{V_{S(\mathrm{空载})} - V_{S(\mathrm{满载})}} {V_{S(\mathrm{空载})}} \times100\% = \frac{24 - 23.45}{24}\times100\% = 2.29\%\approx2.3\%
然后,该变压器的降调百分比计算结果为: 2.29\%,四舍五入后约为 2.3\%。
变压器电压调节示例 2
一台具有 4\% 电压调节的单相变压器,在满负载电流时,其二次端电压为 115.4\,\mathrm{V}。求当负载移除时的空载端电压。
由此可见,连接负载的变化会导致变压器端电压在“空载电压”与“满载电压”之间产生波动,从而使电压调节成为一个由外部负载决定的参数。
因此,百分比电压调节越低,无论负载电流如何变化,变压器二次端电压就越稳定。如果所接负载为纯阻性,则电压降会更小。理想变压器的电压调节为零,即
因为此时不存在任何损耗。
至此,我们知道变压器的电压调节是指在其最大额定二次电流条件下,满载电压与空载电压之差,可表示为比值或百分比( \%)值。但为何二次电压会随着负载电流的变化而变化或下降?
带载状态下的电压变压器
Voltage Transformers On-load
当变压器二次绕组向负载供电时,层压铁芯内会产生磁芯铁损,绕组由于其电阻率会产生铜损,这对一次绕组和二次绕组均适用。 这些损耗在变压器绕组中引入了电抗和电阻,从而形成一条阻抗路径,二次输出电流 I_S 必须流经该路径,如图所示。
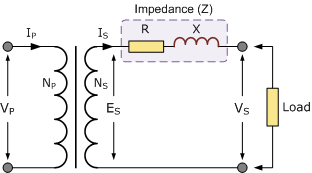
由于二次绕组既包含电阻又包含电抗,因此在变压器绕组中必然会产生内部电压降,其大小取决于等效阻抗和所供给的负载电流,正如欧姆定律所示:
由此可见,随着二次侧负载电流的增加,绕组内的压降也将增大;在一次侧电源电压恒定的情况下,二次输出电压必然下降。
二次绕组的阻抗 Z 是其电阻 R 与漏抗 X 的相量和,在每个分量上都会产生不同的电压降。于是,我们可以将二次阻抗,以及空载和满载电压定义如下:
因此,二次绕组的空载电压定义为:
其满载电压定义为:
显然,变压器绕组由串联的电抗和电阻组成,两者共用同一负载电流。由于电阻上的电压与电流同相,跨电阻的压降 I_S R 与二次电流 I_S 同相;而在纯电感(漏抗 X_L)中,电流相对于电压滞后 90^\circ,故跨电抗的压降 I_S X 相对于电流超前一个角度 \phi_L。由于二次绕组的阻抗 Z 为电阻与电抗的相量和,其各自的相位角可表示为:
由于 V = I \times Z,因此二次侧等效阻抗上的电压降为:
并且由于
则百分比调压可表示为:
滞后功率因数表达式
Lagging Power Factor Expression
当调压表达式中 \cos\Phi 与 \sin\Phi 之间的关系为正时,变压器二次端电压将下降(跌落),表明负载为滞后功率因数(感性负载)。当调压表达式中 \cos\Phi 与 \sin\Phi 之间的关系为负时,变压器二次端电压将上升(升高),表明负载为超前功率因数(容性负载)。因此,变压器的调压表达式对超前和滞后负载都是相同的,仅符号不同,表示电压的升降。
超前功率因数表达式
Leading Power Factor Expression
因此,正的调压条件会在二次绕组中产生电压下降(跌落),而负的调压条件会在绕组中产生电压上升(升高)。尽管超前功率因数负载不像感性负载(线圈、螺线管或扼流圈)那样常见,但当变压器为低电流的小负载供电时,可能会出现电容性状况,导致端电压升高。
变压器电压调节示例 3
一台 10 kVA 单相变压器提供空载二次电压 110 V。当等效二次绕组电阻为 0.015\,\Omega 且总漏抗为 0.04\,\Omega 时,求在滞后功率因数 0.85 负载下的电压调节。
已知数据:
二次侧电流:
百分比电压调节:
变压器电压调节总结
在本教程中,我们讨论了变压器电压调节:当变压器的二次绕组带载时,其输出电压会发生变化,而这种电压变化可以表示为一个比值,或更常用的百分比值。在无载状态下,由于二次侧没有电流流过,二次电压处于最大值。
但是在满载状态下,二次电流流过绕组,产生磁芯损耗和铜损。磁芯损耗是由一次绕组电压在变压器磁路中引起的固定损耗,而二次绕组的铜损则是随着负载电流大小变化的可变损耗。
因此,负载电流的变化会引起损耗的变化,从而影响电压调节。变压器的电压调节越小,二次端电压随负载变化的幅度就越小,这在稳压电源电路中非常有用。
我们还指出,对于滞后功率因数(感性负载),二次端电压会下降;当变压器供给很低的滞后功率因数时,大电流流过二次绕组,因绕组电压降增大而导致电压调节性能变差。对于超前功率因数(容性负载),端电压则会上升。因此,正的调压值对应绕组电压下降,负的调压值对应绕组电压上升。
虽然只有理想变压器才能实现零电压调节,但在实际中,当磁芯损耗与铜损大致相等时,调压最小、效率最高。
附录
电网中避免变压器调节波动的方法
单词表
声明
本文翻译自 electronics-tutorials
本文仅供学习,禁止用于任何的商业用途。

